《2025年寒假零距离七年级数学北师大版》

19. 如图所示，A、B、C是一条公路上的三个村庄，A、B间的路程为100m，A、C间的路程为40m，在A、B之间设有一个车站P，设P、C之间的路程为xm.
（1）用含x的式子表示车站到三个村庄的路程之和；
（2）若车站到三个村庄的路程之和为102m，问车站应设在何处？
（3）若要使车站到三个村庄的路程之和最小，问车站应设在何处？

答案： 三、19. 解：
(1)(x + 100)m；
(2)由题意得，x + 100 = 102，x = 2，所以车站设在朝B村的方向距C村2m处，或者朝A村的方向，距C村2m处；
(3)车站应设在C处.

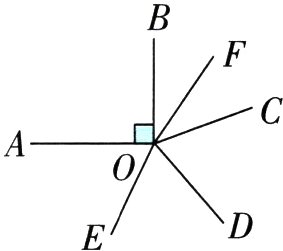
20. 如图所示，由点O引出6条射线OA，OB，OC，OD，OE，OF，且∠AOB=90°，OF平分∠BOC，OE平分∠AOD，若∠EOF=170°，求∠COD的度数.

答案： 三、20. 解：因为∠EOF=170°，∠AOB=90°，所以∠BOF+∠AOE =360° - ∠EOF - ∠AOB=360° - 170° - 90°=100°，又因为OF平分∠BOC，OE平分∠AOD，所以∠COF=∠BOF，∠EOD=∠AOE，所以∠COF+∠EOD=∠BOF+∠AOE =100°，所以∠COD=∠EOF - (∠COF+∠EOD)=170° - 100°=70°.

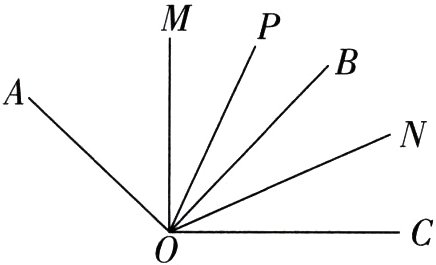
21. 如图，已知OM，ON分别是∠AOB，∠BOC的平分线，射线OP在∠AOC的内部，若要使∠AOP与∠MON相等，则OP应满足什么条件？为什么？

答案： 三、21. 解：OP应满足的条件是OP是∠AOC的平分线. 因为OP平分∠AOC，所以∠AOP=$\frac{1}{2}$∠AOC. 因为OM平分∠AOB，所以∠MOB=$\frac{1}{2}$∠AOB. 又ON平分∠BOC，因为∠NOB=$\frac{1}{2}$∠BOC，所以∠MON=∠MOB+∠NOB=$\frac{1}{2}$(∠AOB+∠BOC)=$\frac{1}{2}$∠AOC，故∠AOP=∠MON.

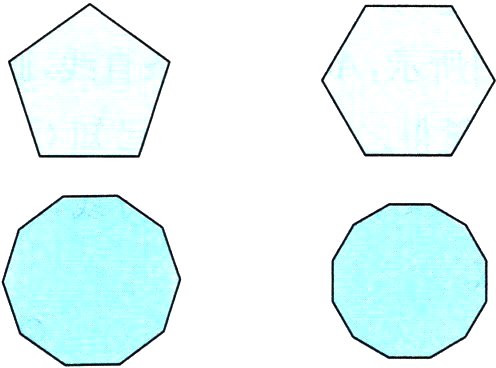
22. 如图所示的多边形分别为正五边形、正六边形、正十边形、正十二边形.
（1）在各正多边形中分别任选一个顶点作对角线，把正多边形分割为若干个三角形；
（2）根据你的分割结果猜想，过正三十边形的一个顶点作对角线，能把正三十边形分割为多少个三角形？
（3）在（2）中，当把正三十边形换为任意三十边形时，结论是否还能成立？

答案：
三、22. 解：
(1)分割情况如图所示.

(2)因为正五边形能分割为3个三角形，正六边形能分割为4个三角形，正十边形能分割为8个三角形，正十二边形能分割为10个三角形，可以猜想：分割成的三角形个数与多边形边数之间的关系为：三角形的个数=多边形的边数 - 2. 所以，正三十边形能分割为28个三角形.
(3)因为分割成的三角形个数只与多边形的边数有关，而与多边形边的长短、角的大小没有关系，所以当把正三十边形换为任意三十边形时，结论仍能成立.