《2025年小学学霸作业本五年级数学下册北师大版》

1. [教材改编]填表。

答案：

2. 选择。
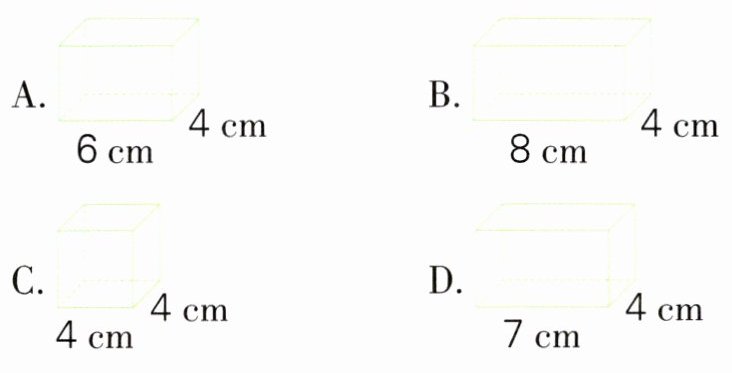
(1)一个底面积是15 dm²的长方体,高减少3 dm,这个长方体的体积减少( )dm³。
A. 75 B. 9 C. 225 D. 45
(2)(名校期末真题)一个内部长8 dm、宽6 dm、高5 dm的长方体纸盒,最多能放( )个棱长为2 dm的正方体木块。
A. 36 B. 30 C. 24 D. 10
(3)在下面四个长方体容器中分别倒入同样多的水(均未满),水位最高的是( )。

答案：
(1)D
(2)C
(3)C

3. [新情境·生活运用]某医院设置了一台长方体自助取药机,为患者提供24时无接触自助取药服务。体积是1.8 m³,占地面积是1.2 m²,这台自助取药机的高是多少米?

答案： $1.8\div1.2 = 1.5(m)$ 答：这台自助取药机的高是1.5 m。

4. 如图是一个无盖长方体玻璃缸,玻璃缸的厚度都是0.1 dm,这个长方体玻璃缸最多能装多少升水?

答案： $5.2 - 0.1\times2 = 5(dm)$ $3.7 - 0.1\times2 = 3.5(dm)$ $4 - 0.1 = 3.9(dm)$ $5\times3.5\times3.9 = 68.25(dm^{3})$ $68.25\ dm^{3}=68.25\ L$ 答：这个长方体玻璃缸最多能装68.25 L水。

5. (名校期末真题)如图,一个长方体水槽被一块玻璃隔板分成A、B两部分。A的底面积为25 dm²,B的底面积为15 dm²,水槽高4 dm。往A部分注满水,将隔板抽出后,这时水槽里的水深多少分米?(隔板厚度不计)
A B

答案： $25\times4\div(25 + 15)=2.5(dm)$ 答：这时水槽里的水深2.5 dm。

6. 一根3.5 m长的长方体木料,沿长垂直切割平均截成4段,表面积比原来增加了1.5 m²。原来这根长方体木料的体积是多少立方米?

答案： $(4 - 1)\times2 = 6(个)$ $1.5\div6\times3.5 = 0.875(m^{3})$ 答：原来这根长方体木料的体积是$0.875\ m^{3}$。 解析：截成4段，增加了6个截面的面积，先求出一个截面的面积，再用截面的面积乘长即可求出原来木料的体积。

7. 一个长方体的表面积是150 cm²,底面积是35 cm²,底面的周长是16 cm,这个长方体的体积是多少?

答案： $150 - 35\times2 = 80(cm^{2})$ $80\div16 = 5(cm)$ $35\times5 = 175(cm^{3})$ 答：这个长方体的体积是$175\ cm^{3}$。 解析：用表面积减去2个底面积，得到侧面的面积，是$150 - 35\times2 = 80(cm^{2})$，侧面展开后的长是底面周长16 cm，则侧面展开后的宽是$80\div16 = 5(cm)$，所以长方体的高是5 cm，再根据长方体的体积 = 底面积×高得出体积。

0.7×0.7×0.7= 25×5×4= 6×6×2= 5×7×8=

答案： 0.343 500 72 280