《2025年小学学霸作业本五年级数学下册北师大版》

1. 填空。
(1)棱长是1 cm的正方体,体积是1( )。
(2)棱长是1 dm的正方体,体积是1( )。
(3)棱长是1 m的正方体,体积是1( )。
(4)米是( )单位,平方米是( )单位,立方米是( )单位。

答案：
(1)$cm^{3}$
(2)$dm^{3}$
(3)$m^{3}$
(4)长度 面积 体积

2. 选择。
(1)棱长是1 dm的正方体,它的体积与表面积的关系是( )。
A. 体积大于表面积 B. 体积小于表面积
C. 体积等于表面积 D. 无法比较
(2)30箱苹果大约可以占2( )的空间。
A. m³ B. cm³
C. dm³ D. 都不正确
(3)一个纸盒中正好可以放12个棱长是1 cm的小正方体且无空隙,若纸盒的厚度不计,这个纸盒的体积是( )。
A. 12 cm² B. 24 cm³
C. 12 cm³ D. 无法确定

答案：
(1)D
(2)A
(3)C

3. 在( )里填上合适的体积单位。
 
 

答案： $dm^{3}$ $cm^{3}$ $m^{3}$ $cm^{3}$ $dm^{3}$ $cm^{3}$

4. 下列图形都是用1 cm³的正方体搭成的,它们的体积各是多少?

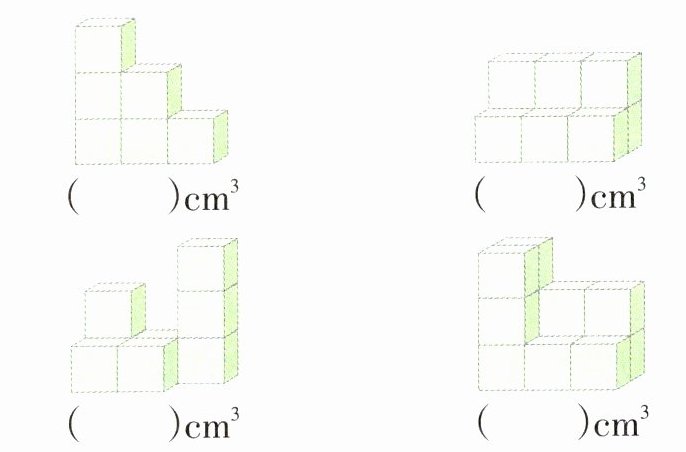
答案： 6 9 8 12

5. 如图,下面的长方体木块都是用体积是1 cm³的小正方体木块摆成的,分别计算两个长方体木块的体积。

______________

答案： $36\ cm^{3}$ $48\ cm^{3}$

6. 用几个体积是1 cm³的小正方体搭成一个立体图形,从正面、上面和侧面看到的形状如下图,计算这个立体图形的体积。

答案： 这个立体图形的体积是$6\ cm^{3}$。

7. 每个小正方体的棱长都是1 cm,至少还需要增加多少个小正方体才能使它成为一个大正方体? 大正方体的体积是多少?

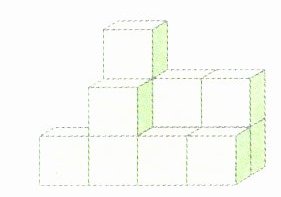
答案： $4×4×4 = 64$(个) $64 - 12 = 52$(个) $1×1×1×64 = 64(cm^{3})$ 答：至少还需要增加52个小正方体才能使它成为一个大正方体，大正方体的体积是$64\ cm^{3}$。 解析：要补成一个大正方体，每层至少有$(4×4)$个小正方体，有4层，所以大正方体有$4×4×4 = 64$(个)小正方体，已经有12个，还需要增加$64 - 12 = 52$(个)。每个小正方体的体积是$1×1×1 = 1(cm^{3})$，所以大正方体的体积是$64\ cm^{3}$。

12×2×7= 0.4×4×4= 3×0.7×0.3= 0.3×5×2=

答案： 168 6.4 0.63 3