《2025年启东中学作业本八年级数学下册江苏版》

1. 某运输公司运输一批货物，已知大货车比小货车每辆多运输5吨货物，且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同，设每辆大货车运输x吨，则所列方程正确的是 （ ）
A. $\frac{75}{x - 5}=\frac{50}{x}$
B. $\frac{75}{x}=\frac{50}{x - 5}$
C. $\frac{75}{x + 5}=\frac{50}{x}$
D. $\frac{75}{x}=\frac{50}{x + 5}$

答案： 1.B

2. 学校最近新配备了一批图书需要甲、乙两人进行整理，若甲单独整理需要4小时完工；若甲、乙共同整理2小时后，乙再单独整理2小时才能完工，则乙单独整理完成需要 （ ）
A. 4小时
B. 6小时
C. 8小时
D. 10小时

答案： 2.C

3.（2023·东台月考）为了改善生态环境，林业局计划在荒坡上种树960棵，由于青年志愿者支援，实际每天种树的棵数是原计划的2倍，结果提前4天完成任务，则原计划每天种树的棵数是_______.

答案： 3.120棵

4. 某商店第一次用600元购进2B铅笔若干枝，第二次又用600元购进该种铅笔，但这次每枝的进价是第一次进价的$\frac{5}{4}$倍，购进数量比第一次少了30枝，则该商店第一次购进的铅笔每枝的进价是_______元.

答案： 4.4

5. 某地计划在规定时间内种植梨树6000棵. 开始种植时，由于志愿者的加入，实际每天种植梨树的数量比原计划增加了20％，结果提前2天完成任务. 问原计划每天种植梨树多少棵?

答案： 5.解:设原计划每天种植梨树$x$棵，则实际每天种植梨树$(1 + 20\%)x$棵，
　根据题意，得$\frac{6000}{x}-\frac{6000}{(1 + 20\%)x}=2$，
　解得$x = 500$，
　经检验，$x = 500$是所列方程的解，且符合题意.
　答:原计划每天种植梨树500棵.

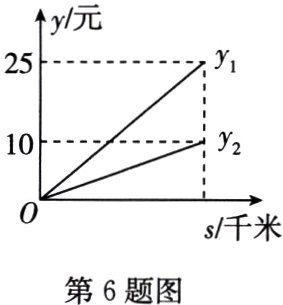
6.（2023·广安）为了降低成本，某出租车公司实施了“油改气”措施. 如图，$y_1$，$y_2$分别表示燃油汽车和燃气汽车所需费用y（单位：元）与行驶路程s（单位：千米）的关系，已知燃油汽车每千米所需的费用比燃气汽车每千米所需的费用的3倍少0.1元，设燃气汽车每千米所需的费用为x元，则可列方程为 （ ）

A. $\frac{25}{x}=\frac{10}{3x - 0.1}$
B. $\frac{25}{x}=\frac{10}{3x + 0.1}$
C. $\frac{25}{3x + 0.1}=\frac{10}{x}$
D. $\frac{25}{3x - 0.1}=\frac{10}{x}$

答案： 6.D