《2025年启东中学作业本八年级数学下册江苏版》

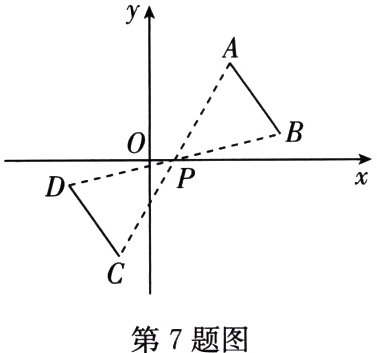
7.（2023·江宁区月考）如图，线段AB与线段CD关于点P对称，若点A(a，b)，B(5，1)，D(－3，－1)，则点C的坐标为（ ）
A.(－a，－b)
B.(－a＋2，－b)
C.(－a－1，－b＋1)
D.(－a＋1，－b－1)
　　　

答案： B

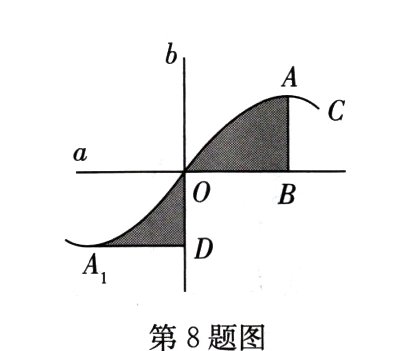
8.如图，直线a，b互相垂直，垂足为O，曲线C关于点O成中心对称，点A的对称点是A₁，AB⊥a于点B，A₁D⊥b于点D，若OB=5，OD=3，则阴影部分的面积之和为________.
　　　

答案： 15

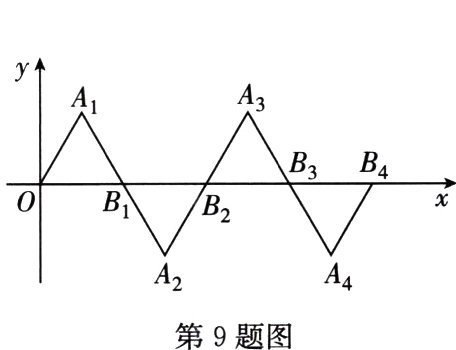
9.在如图所示的平面直角坐标系中，△OA₁B₁是边长为2的等边三角形，作△B₁A₂B₂与△OA₁B₁关于点B₁成中心对称，再作△B₂A₃B₃与△B₁A₂B₂关于点B₂成中心对称，如此作下去，则△B₂₀A₂₁B₂₁的顶点A₂₁的坐标是________.
　　　

答案： $(41,\sqrt{3})$

10.（2023·沭阳县月考）如图，△ABM与△ACM关于直线AF成轴对称，△ABE与△DCE关于点E成中心对称，点E，D，M都在线段AF上，BM的延长线交CF于点P.
（1）求证：AC=CD；
（2）若∠BAC=2∠MPC，请判断∠F与∠MCD的数量关系，并说明理由.
　　　

答案：
(1) 证明：$\because \triangle ABM$与$\triangle ACM$关于直线$AF$成轴对称，
$\therefore \triangle ABM \cong \triangle ACM$，$\therefore AB = AC$.
又$\because \triangle ABE$与$\triangle DCE$关于点$E$成中心对称，
$\therefore \triangle ABE \cong \triangle DCE$，$\therefore AB = CD$，$\therefore AC = CD$.
(2) 解：$\angle F = \angle MCD$.
理由：由
(1) 可得$\angle BAE = \angle CAE = \angle CDE$，$\angle CMA = \angle BMA$，
$\because \angle BAC = 2\angle MPC$，$\angle BMA = \angle PMF$，
$\therefore$设$\angle MPC = \alpha$，则$\angle BAE = \angle CAE = \angle CDE = \alpha$.
设$\angle BMA = \beta$，则$\angle PMF = \angle CMA = \beta$，
$\therefore \angle F = \angle CPM - \angle PMF = \alpha - \beta$，
$\angle MCD = \angle CDE - \angle DMC = \alpha - \beta$，$\therefore \angle F = \angle MCD$.

11.知识背景：过中心对称图形的对称中心的任意一条直线都将其分成面积相等的两个部分.
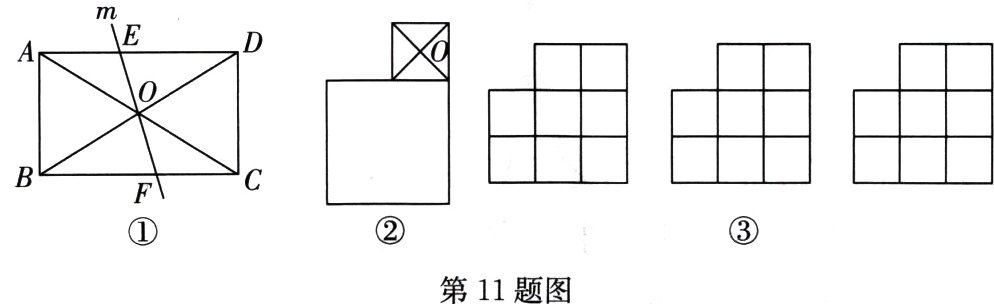
（1）如图①，直线m经过长方形ABCD对角线的交点O，则$S_{四边形AEFB}________S_{四边形DEFC}；$（填“＞”“＜”或“＝”）
（2）如图②，两个正方形如图所示摆放，O为小正方形对角线的交点，求作过点O的直线将整个图形分成面积相等的两部分；
（3）八个大小相同的正方形如图③所示摆放，求作直线将整个图形分成面积相等的两部分.（用三种方法分割）
　　　　　　　　　

答案：

(1) $=$
(2) 解：如答图①所示.
(3) 解：如答图②所示.