第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
23. (11分)如图,在△ABD中,∠ABC=45°,AC,BF为△ABD的两条高.
(1)求证:BE=AD;
(2)若过点C作CM//AB,交AD于点M,求证:BE=AM+EM.
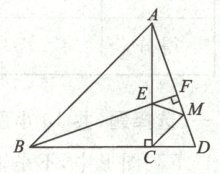
(1)求证:BE=AD;
(2)若过点C作CM//AB,交AD于点M,求证:BE=AM+EM.

答案:
(1)证明:
∵AC、BF为△ABD的高,
∴∠ACB=∠ACD=∠AFB=90°.
∵∠ABC=45°,
∴Rt△ABC是等腰直角三角形,
∴AC=BC.
∵∠BEC=∠AED(对顶角相等),∠BEC+∠EBC=90°,∠AED+∠EAD=90°,
∴∠EBC=∠EAD(等角的余角相等).
在△BEC和△ADC中,
$\left\{\begin{array}{l} ∠EBC=∠DAC\\ BC=AC\\ ∠BCE=∠ACD=90°\end{array}\right.$,
∴△BEC≌△ADC(ASA),
∴BE=AD.
(2)证明:
∵CM//AB,
∴∠BAC=∠MCA(两直线平行,内错角相等).
∵∠BAC=45°(Rt△ABC中,∠ABC=45°),
∴∠MCA=45°.
∵∠ACD=90°,
∴∠MCD=∠ACD-∠MCA=45°,
∴∠MCA=∠MCD=45°.
由
(1)△BEC≌△ADC得EC=DC.
在△CEM和△CDM中,
$\left\{\begin{array}{l} EC=DC\\ ∠ECM=∠DCM=45°\\ CM=CM\end{array}\right.$,
∴△CEM≌△CDM(SAS),
∴EM=DM.
∵AD=AM+DM,
∴AD=AM+EM.
∵BE=AD(由
(1)得),
∴BE=AM+EM.
(1)证明:
∵AC、BF为△ABD的高,
∴∠ACB=∠ACD=∠AFB=90°.
∵∠ABC=45°,
∴Rt△ABC是等腰直角三角形,
∴AC=BC.
∵∠BEC=∠AED(对顶角相等),∠BEC+∠EBC=90°,∠AED+∠EAD=90°,
∴∠EBC=∠EAD(等角的余角相等).
在△BEC和△ADC中,
$\left\{\begin{array}{l} ∠EBC=∠DAC\\ BC=AC\\ ∠BCE=∠ACD=90°\end{array}\right.$,
∴△BEC≌△ADC(ASA),
∴BE=AD.
(2)证明:
∵CM//AB,
∴∠BAC=∠MCA(两直线平行,内错角相等).
∵∠BAC=45°(Rt△ABC中,∠ABC=45°),
∴∠MCA=45°.
∵∠ACD=90°,
∴∠MCD=∠ACD-∠MCA=45°,
∴∠MCA=∠MCD=45°.
由
(1)△BEC≌△ADC得EC=DC.
在△CEM和△CDM中,
$\left\{\begin{array}{l} EC=DC\\ ∠ECM=∠DCM=45°\\ CM=CM\end{array}\right.$,
∴△CEM≌△CDM(SAS),
∴EM=DM.
∵AD=AM+DM,
∴AD=AM+EM.
∵BE=AD(由
(1)得),
∴BE=AM+EM.
24. (12分)已知在四边形ABCD中,AB=AD,∠EAF=$\frac{1}{2}$∠BAD.
(1)如图1,∠ABC=∠ADC=90°,E,F分别是边BC,CD上的点,则线段EF,BE,FD之间的关系是
(2)如图2,∠ABC+∠ADC=180°,E,F分别是边BC,CD上的点,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.

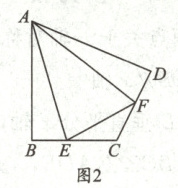
(1)如图1,∠ABC=∠ADC=90°,E,F分别是边BC,CD上的点,则线段EF,BE,FD之间的关系是
$EF = BE + FD$
;(2)如图2,∠ABC+∠ADC=180°,E,F分别是边BC,CD上的点,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.


答案:
(1) $EF = BE + FD$
(2) 结论仍然成立,证明如下:
延长 $FD$ 到点 $G$,使 $DG = BE$,连接 $AG$。
在 $\triangle ABE$ 和 $\triangle ADG$ 中:
$AB = AD$,$\angle ABE = \angle ADG = 180° - \angle ADC$,$BE = DG$,
所以 $\triangle ABE \cong \triangle ADG$(SAS)。
则 $AE = AG$,$\angle BAE = \angle DAG$。
因为 $\angle EAF = \frac{1}{2}\angle BAD$,
所以 $\angle GAF = \angle DAG + \angle DAF = \angle BAE + \angle DAF = \angle BAD - \angle EAF = \angle EAF$。
在 $\triangle AEF$ 和 $\triangle AGF$ 中:
$AE = AG$,$\angle EAF = \angle GAF$,$AF = AF$,
所以 $\triangle AEF \cong \triangle AGF$(SAS)。
则 $EF = GF$。
因为 $GF = DG + FD = BE + FD$,
所以 $EF = BE + FD$。
(1) $EF = BE + FD$
(2) 结论仍然成立,证明如下:
延长 $FD$ 到点 $G$,使 $DG = BE$,连接 $AG$。
在 $\triangle ABE$ 和 $\triangle ADG$ 中:
$AB = AD$,$\angle ABE = \angle ADG = 180° - \angle ADC$,$BE = DG$,
所以 $\triangle ABE \cong \triangle ADG$(SAS)。
则 $AE = AG$,$\angle BAE = \angle DAG$。
因为 $\angle EAF = \frac{1}{2}\angle BAD$,
所以 $\angle GAF = \angle DAG + \angle DAF = \angle BAE + \angle DAF = \angle BAD - \angle EAF = \angle EAF$。
在 $\triangle AEF$ 和 $\triangle AGF$ 中:
$AE = AG$,$\angle EAF = \angle GAF$,$AF = AF$,
所以 $\triangle AEF \cong \triangle AGF$(SAS)。
则 $EF = GF$。
因为 $GF = DG + FD = BE + FD$,
所以 $EF = BE + FD$。
查看更多完整答案,请扫码查看


