2025年练习生高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [2022·河北石家庄高二期末]使函数$f(x)=x+\sqrt{2}\cos x$在$\left[0,\frac{\pi}{2}\right]$上取得最大值的$x$为 (
A.$0$
B.$\frac{\pi}{4}$
C.$\frac{\pi}{3}$
D.$\frac{\pi}{2}$
B
)A.$0$
B.$\frac{\pi}{4}$
C.$\frac{\pi}{3}$
D.$\frac{\pi}{2}$
答案:
1.B【解析】由题意,得$f'(x)=1-\sqrt{2}\sin x$.令$f'(x)>0$,得$\sin x<\frac{\sqrt{2}}{2}$.因为$x\in\left[0,\frac{\pi}{2}\right]$,所以当$f'(x)>0$时,$x\in\left[0,\frac{\pi}{4}\right)$.令$f'(x)<0$,得$\sin x>\frac{\sqrt{2}}{2}$,所以$x\in\left(\frac{\pi}{4},\frac{\pi}{2}\right]$.所以$f(x)$在$\left[0,\frac{\pi}{4}\right)$上单调递增,在$\left(\frac{\pi}{4},\frac{\pi}{2}\right]$上单调递减,所以使$f(x)$在$\left[0,\frac{\pi}{2}\right]$上取得最大值的$x$为$\frac{\pi}{4}$(该值也叫做函数的最值点).故选B.
2. (多选)[2023·福建南平高二期末]若函数$f(x)=\mathrm{e}^{x}-2x+3$,则 (
A. 函数$f(x)$只有极大值没有极小值
B. 函数$f(x)$只有最大值没有最小值
C. 函数$f(x)$只有极小值没有极大值
D. 函数$f(x)$只有最小值没有最大值
CD
)A. 函数$f(x)$只有极大值没有极小值
B. 函数$f(x)$只有最大值没有最小值
C. 函数$f(x)$只有极小值没有极大值
D. 函数$f(x)$只有最小值没有最大值
答案:
2.CD【解析】由题意得$f'(x)=e^x-2$.令$f'(x)=0$,得$x=\ln2$.则当$x\in(-\infty,\ln2)$时,$f'(x)<0$,此时$f(x)$单调递减;当$x\in(\ln2,+\infty)$时,$f'(x)>0$,此时$f(x)$单调递增.所以函数$f(x)$有唯一极小值,也是最小值,没有极大值和最大值.故选CD.
方法总结 当函数在某区间上有唯一极值时,该极值也是最值.
方法总结 当函数在某区间上有唯一极值时,该极值也是最值.
3. [2023·陕西汉中兴华中学、镇巴中学高二期中联考]设$f'(x)$是函数$f(x)$的导函数,$y=f'(x)$的图像如图,则下列说法正确的序号是
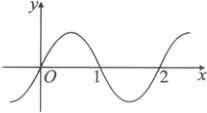
(1) 函数$f(x)$一定有$3$个零点;
(2) 函数$f(x)$一定有$3$个极值点;
(3) 函数$f(x)$有最小值;
(4) 函数$f(x)$有最大值;
(5) 函数$f(x)$的图像一定经过原点.
题型 2 求函数的最值
(2)(3)
.
(1) 函数$f(x)$一定有$3$个零点;
(2) 函数$f(x)$一定有$3$个极值点;
(3) 函数$f(x)$有最小值;
(4) 函数$f(x)$有最大值;
(5) 函数$f(x)$的图像一定经过原点.
题型 2 求函数的最值
答案:
3.
(2)
(3)【解析】根据题图知,当$x\in(-\infty,0)$时,$f'(x)<0$,此时函数$f(x)$单调递减;当$x\in(0,1)$时,$f'(x)>0$,此时函数$f(x)$单调递增;当$x\in(1,2)$时,$f'(x)<0$,此时函数$f(x)$单调递减;当$x\in(2,+\infty)$时,$f'(x)>0$,此时函数$f(x)$单调递增.所以$x=0,x=1,x=2$均是函数$f(x)$的极值点,故
(2)正确.函数$f(x)$的图像可能都在$x$轴上方,其零点个数可能是0,故
(1)错误.函数$f(x)$的图像不一定经过原点,故
(5)错误.由定义可知,$x=0$和$x=2$都是函数$f(x)$的极小值点,所以$f(0),f(2)$都是函数$f(x)$的极小值,因此函数有最小值,且为$f(0),f(2)$中的较小者,无最大值,所以
(3)正确,
(4)错误.
(2)
(3)【解析】根据题图知,当$x\in(-\infty,0)$时,$f'(x)<0$,此时函数$f(x)$单调递减;当$x\in(0,1)$时,$f'(x)>0$,此时函数$f(x)$单调递增;当$x\in(1,2)$时,$f'(x)<0$,此时函数$f(x)$单调递减;当$x\in(2,+\infty)$时,$f'(x)>0$,此时函数$f(x)$单调递增.所以$x=0,x=1,x=2$均是函数$f(x)$的极值点,故
(2)正确.函数$f(x)$的图像可能都在$x$轴上方,其零点个数可能是0,故
(1)错误.函数$f(x)$的图像不一定经过原点,故
(5)错误.由定义可知,$x=0$和$x=2$都是函数$f(x)$的极小值点,所以$f(0),f(2)$都是函数$f(x)$的极小值,因此函数有最小值,且为$f(0),f(2)$中的较小者,无最大值,所以
(3)正确,
(4)错误.
4. 函数$f(x)=\ln x+\frac{1}{2x^{2}}+3$的最小值是 (
A.$\frac{9}{2}$
B.$4$
C.$\frac{7}{2}$
D.$3$
C
)A.$\frac{9}{2}$
B.$4$
C.$\frac{7}{2}$
D.$3$
答案:
4.C【解析】由题意得$f'(x)=\frac{1}{x}-\frac{1}{x^3}=\frac{x^2-1}{x^3}(x>0)$.令$f'(x)>0$,得$x>1$;令$f'(x)<0$,得$0<x<1$.则$f(x)$在$(0,1)$上单调递减,在$(1,+\infty)$上单调递增,故$f(x)$的最小值是$f(1)=\frac{7}{2}$(利用导数讨论函数的单调性,确定函数的极值,验证是否为最值).故选C.
5. [2023·河南大联考高二阶段性测试]函数$f(x)=x-3x^{3},x\in[0,1]$的最大值是 (
A.$-\frac{2}{9}$
B.$\frac{2}{9}$
C.$0$
D.$1$
B
)A.$-\frac{2}{9}$
B.$\frac{2}{9}$
C.$0$
D.$1$
答案:
5.B【解析】由题意得$f'(x)=1-9x^2(0\leqslant x\leqslant1)$.当$x\in\left[0,\frac{1}{3}\right)$时,$f'(x)>0$,此时$f(x)$单调递增;当$x\in\left(\frac{1}{3},1\right]$时,$f'(x)<0$,此时$f(x)$单调递减.故当$x=\frac{1}{3}$时,$f(x)$取得极大值,也是最大值(此题若求闭区间上函数的最小值,要注意端点值),且最大值为$f\left(\frac{1}{3}\right)=\frac{1}{3}-3×\left(\frac{1}{3}\right)^3=\frac{1}{3}-\frac{1}{9}=\frac{2}{9}$.故选B.
6. [2023·浙江杭州之江高级中学高二期中]函数$f(x)=x\ln x$在$(0,\mathrm{e}]$上的最小值是
$-\frac{1}{e}$
.
答案:
6.$-\frac{1}{e}$【解析】由题意得$f'(x)=\ln x+1$.因为$0<x\leqslant e$,所以令$f'(x)>0$,得$\frac{1}{e}<x\leqslant e$;令$f'(x)<0$,得$0<x<\frac{1}{e}$.所以$f(x)=x\ln x$在$\left(0,\frac{1}{e}\right)$上单调递减,在$\left(\frac{1}{e},e\right]$上单调递增,所以$f(x)=x\ln x$在$(0,e]$上的最小值是$f\left(\frac{1}{e}\right)=-\frac{1}{e}$.
7. [2023·陕西咸阳高二期末]已知函数$f(x)=-x^{3}+ax^{2}+bx-5$在$x=-1$处有极值$-1$.
(1)求实数$a,b$的值;
(2)求函数$f(x)$在$[-4,2]$上的最值.
(1)求实数$a,b$的值;
(2)求函数$f(x)$在$[-4,2]$上的最值.
答案:
7.思维路径
(1)求出函数的导数→根据题意列出方程组→求得$a,b$的值.
(2)求出函数的极值点→求得函数的极值以及区间端点处的函数值→比较可得函数的最值.
【解】
(1)由题意,得$f'(x)=-3x^2+2ax+b$.
∵函数$f(x)$在$x=-1$处有极值$-1$,
∴$\begin{cases}f(-1)=a-b-4=-1,\\f'(-1)=-2a+b-3=0,\end{cases}$解得$\begin{cases}a=-6,\\b=-9.\end{cases}$
∴$f'(x)=-3x^2-12x-9=-3(x+1)(x+3)$.
若$f'(x)>0$,则$-3<x<-1$;若$f'(x)<0$,则$x<-3$或$x>-1$.
∴函数$f(x)$在$x=-1$处有极大值,且极大值为$-1$,符合题意,
故$a=-6,b=-9$.
(2)由
(1)知$f(x)=-x^3-6x^2-9x-5$,
∴$f'(x)=-3x^2-12x-9=-3(x+1)(x+3)$.
若$f'(x)>0$,则$-3<x<-1$;若$f'(x)<0$,则$x<-3$或$x>-1$.
又
∵$-4\leqslant x\leqslant2$,
∴$f(x)$在$(-3,-1)$上单调递增,在$[-4,-3),(-1,2]$上单调递减.
又$f(-4)=-5,f(-3)=-5,f(-1)=-1,f(2)=-55$,
∴$f(x)_{max}=-1,f(x)_{min}=-55$.
(1)求出函数的导数→根据题意列出方程组→求得$a,b$的值.
(2)求出函数的极值点→求得函数的极值以及区间端点处的函数值→比较可得函数的最值.
【解】
(1)由题意,得$f'(x)=-3x^2+2ax+b$.
∵函数$f(x)$在$x=-1$处有极值$-1$,
∴$\begin{cases}f(-1)=a-b-4=-1,\\f'(-1)=-2a+b-3=0,\end{cases}$解得$\begin{cases}a=-6,\\b=-9.\end{cases}$
∴$f'(x)=-3x^2-12x-9=-3(x+1)(x+3)$.
若$f'(x)>0$,则$-3<x<-1$;若$f'(x)<0$,则$x<-3$或$x>-1$.
∴函数$f(x)$在$x=-1$处有极大值,且极大值为$-1$,符合题意,
故$a=-6,b=-9$.
(2)由
(1)知$f(x)=-x^3-6x^2-9x-5$,
∴$f'(x)=-3x^2-12x-9=-3(x+1)(x+3)$.
若$f'(x)>0$,则$-3<x<-1$;若$f'(x)<0$,则$x<-3$或$x>-1$.
又
∵$-4\leqslant x\leqslant2$,
∴$f(x)$在$(-3,-1)$上单调递增,在$[-4,-3),(-1,2]$上单调递减.
又$f(-4)=-5,f(-3)=-5,f(-1)=-1,f(2)=-55$,
∴$f(x)_{max}=-1,f(x)_{min}=-55$.
8. [2022·北京高二期中]函数$f(x)=\frac{1}{3}x^{3}-x^{2}$在区间$(a,a+5)$内存在最小值,则实数$a$的取值范围是 (
A.$(-3,2)$
B.$[-3,2)$
C.$[-1,2)$
D.$(-1,2)$
C
)A.$(-3,2)$
B.$[-3,2)$
C.$[-1,2)$
D.$(-1,2)$
答案:
8.C【解析】由题意得$f'(x)=x^2-2x$.令$f'(x)=0$,得$x_1=0$,$x_2=2$,则当$x\in(-\infty,0)\cup(2,+\infty)$时,$f'(x)>0$,此时$f(x)$单调递增;当$x\in(0,2)$时,$f'(x)<0$,此时$f(x)$单调递减.
易得$f(-1)=-\frac{4}{3},f(0)=0,f(2)=-\frac{4}{3}$.作出$f(x)$的大致图像,如图.因为$f(x)$在区间$(a,a+5)$内存在最小值(注意区间为开区间,端点值取不到,可转化为该区间内的极小值点就是最小值点),所以最小值为$f(2)$.又$f(-1)=f(2)$,所以$\begin{cases}-1\leqslant a<2,\\a+5>2,\end{cases}$解得$-1\leqslant a<2$.故选C.

8.C【解析】由题意得$f'(x)=x^2-2x$.令$f'(x)=0$,得$x_1=0$,$x_2=2$,则当$x\in(-\infty,0)\cup(2,+\infty)$时,$f'(x)>0$,此时$f(x)$单调递增;当$x\in(0,2)$时,$f'(x)<0$,此时$f(x)$单调递减.
易得$f(-1)=-\frac{4}{3},f(0)=0,f(2)=-\frac{4}{3}$.作出$f(x)$的大致图像,如图.因为$f(x)$在区间$(a,a+5)$内存在最小值(注意区间为开区间,端点值取不到,可转化为该区间内的极小值点就是最小值点),所以最小值为$f(2)$.又$f(-1)=f(2)$,所以$\begin{cases}-1\leqslant a<2,\\a+5>2,\end{cases}$解得$-1\leqslant a<2$.故选C.

9. (多选)[2023·山西大同一中高二期末]已知函数$f(x)=ax^{4}-4ax^{3}+b,x\in[1,4],f(x)$的最大值为$3$,最小值为$-6$,则$a+b$的值可能为 (
A.$-\frac{19}{3}$
B.$-\frac{10}{3}$
C.$\frac{10}{3}$
D.$\frac{19}{3}$
AC
)A.$-\frac{19}{3}$
B.$-\frac{10}{3}$
C.$\frac{10}{3}$
D.$\frac{19}{3}$
答案:
9.AC【解析】由题意得$f'(x)=4ax^2(x-3),1\leqslant x\leqslant4$.当$a=0$时(注意讨论参数$a$),$f(x)=b$,显然不合题意,舍去;当$a>0$时,令$f'(x)>0$,得$x>3$.又$1\leqslant x\leqslant4$,所以$3<x\leqslant4$.令$f'(x)<0$,得$x<3$.又$1\leqslant x\leqslant4$,所以$1\leqslant x<3$.故$f(x)$在$(3,4]$上单调递增,在$[1,3)$上单调递减,且$f(3)=b-27a$,$f(1)=b-3a,f(4)=b$,即$f(1)<f(4)$,故$\begin{cases}b-27a=-6,\\b=3,\end{cases}$解得$\begin{cases}a=\frac{1}{3},\\b=3,\end{cases}$则$a+b=\frac{10}{3}$.当$a<0$时,令$f'(x)>0$,得$x<3$.又$1\leqslant x\leqslant4$,所以$1\leqslant x<3$.令$f'(x)<0$,得$x>3$.又$1\leqslant x\leqslant4$,所以$3<x\leqslant4$.故$f(x)$在$[1,3)$上单调递增,在$(3,4]$上单调递减,且$f(3)=b-27a,f(1)=b-3a,f(4)=b$,即$f(1)>f(4)$,故$\begin{cases}b-27a=3,\\b=-6,\end{cases}$解得$\begin{cases}a=\frac{1}{3},\\b=-6,\end{cases}$则$a+b=-\frac{19}{3}$.综上所述,$a+b=\frac{10}{3}$或$a+b=-\frac{19}{3}$.故选AC.
10. [2023·江苏南京第一中学高二月考]已知函数$f(x)=-\frac{1}{3}x^{3}+x^{2}+3x+a$.
(1)求$f(x)$的单调区间;
(2)若$f(x)$在区间$[-3,3]$上的最小值为$\frac{7}{3}$,求$a$的值.
(1)求$f(x)$的单调区间;
(2)若$f(x)$在区间$[-3,3]$上的最小值为$\frac{7}{3}$,求$a$的值.
答案:
10.思维路径
(1)求出导数→令$f'(x)>0,f'(x)<0$,分别解不等式→求出函数的单调区间.
(2)求得$f(x)$在区间$[-3,3]$内的单调区间→求得极值→求出端点处的函数值→比较得函数的最小值→解方程求得$a$的值.
【解】
(1)由题意,得$f'(x)=-x^2+2x+3$.
令$f'(x)>0$,得$-1<x<3$;令$f'(x)<0$,得$x<-1$或$x>3$.
所以$f(x)$的单调递减区间为$(-\infty,-1)$和$(3,+\infty)$,单调递增区间为$(-1,3)$.
(2)结合
(1)知,当$x$在区间$[-3,3]$内变化时,$f'(x),f(x)$的变化情况如下表.
$x$ $-3$ $(-3,-1)$ $-1$ $(-1,3)$ $3$
$f'(x)$ $-$ $-$ $0$ $+$ $0$
$f(x)$ $f(-3)$ 单调递减 极小值 单调递增 $f(3)$
所以函数$f(x)$在$(-3,-1)$上单调递减,在$(-1,3)$上单调递增.
所以$f(x)\geqslant f(-1)$,所以$f(x)$的最小值为$f(-1)=\frac{1}{3}+1-3+a=\frac{7}{3}$,解得$a=4$.
(1)求出导数→令$f'(x)>0,f'(x)<0$,分别解不等式→求出函数的单调区间.
(2)求得$f(x)$在区间$[-3,3]$内的单调区间→求得极值→求出端点处的函数值→比较得函数的最小值→解方程求得$a$的值.
【解】
(1)由题意,得$f'(x)=-x^2+2x+3$.
令$f'(x)>0$,得$-1<x<3$;令$f'(x)<0$,得$x<-1$或$x>3$.
所以$f(x)$的单调递减区间为$(-\infty,-1)$和$(3,+\infty)$,单调递增区间为$(-1,3)$.
(2)结合
(1)知,当$x$在区间$[-3,3]$内变化时,$f'(x),f(x)$的变化情况如下表.
$x$ $-3$ $(-3,-1)$ $-1$ $(-1,3)$ $3$
$f'(x)$ $-$ $-$ $0$ $+$ $0$
$f(x)$ $f(-3)$ 单调递减 极小值 单调递增 $f(3)$
所以函数$f(x)$在$(-3,-1)$上单调递减,在$(-1,3)$上单调递增.
所以$f(x)\geqslant f(-1)$,所以$f(x)$的最小值为$f(-1)=\frac{1}{3}+1-3+a=\frac{7}{3}$,解得$a=4$.
查看更多完整答案,请扫码查看


