2025年练习生高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. [2023·吉林长春东北师范大学附属中学高二期
中]下列函数中,在$(0,+\infty)$上为增函数的是
(
A. $y=\sin x-x$
B. $y=x-\ln x$
C. $y=e^{x}-x$
D. $y=x+\frac{1}{x}$
中]下列函数中,在$(0,+\infty)$上为增函数的是
(
C
)A. $y=\sin x-x$
B. $y=x-\ln x$
C. $y=e^{x}-x$
D. $y=x+\frac{1}{x}$
答案:
1.C【解析】对于A,$y'=\cos x - 1\leq0$,则$y = \sin x - x$在定义域$\mathbf{R}$上单调递减,故A不符合题意.对于B,$y' = 1 - \frac{1}{x}=\frac{x - 1}{x}(x>0)$,所以当$x>1$时,$y'>0$;当$0<x<1$时,$y'<0$.所以函数$y = x - \ln x$在$(0,1)$上单调递减,在$(1,+\infty)$上单调递增,故B不符合题意.对于C,$y' = e^x - 1$,所以当$x>0$时,$y'>0$,所以函数$y = e^x - x$在$(0,+\infty)$上单调递增,故C符合题意.对于D,$y' = 1 - \frac{1}{x^2}=\frac{x^2 - 1}{x^2}=\frac{(x - 1)(x + 1)}{x^2}$,所以当$x>1$时,$y'>0$;当$0<x<1$时,$y'<0$.所以函数$y = x + \frac{1}{x}$在$(0,1)$上单调递减,在$(1,+\infty)$上单调递增,故D不符合题意.选C.
2. [2023·天津南开中学高二期中]以下关于函数$y=\sin x-x+1,x\in(0,\pi)$的单调性的判断正确的是
(
A. 在$(0,\pi)$上单调递增
B. 在$(0,\pi)$上单调递减
C. 在$\left(0,\frac{\pi}{2}\right)$上单调递增,在$\left(\frac{\pi}{2},\pi\right)$上单调递减
D. 在$\left(0,\frac{\pi}{2}\right)$上单调递减,在$\left(\frac{\pi}{2},\pi\right)$上单调递增
(
B
)A. 在$(0,\pi)$上单调递增
B. 在$(0,\pi)$上单调递减
C. 在$\left(0,\frac{\pi}{2}\right)$上单调递增,在$\left(\frac{\pi}{2},\pi\right)$上单调递减
D. 在$\left(0,\frac{\pi}{2}\right)$上单调递减,在$\left(\frac{\pi}{2},\pi\right)$上单调递增
答案:
2.B【解析】由题意,得$y' = \cos x - 1$.因为$x\in(0,\pi)$,所以$\cos x\in(-1,1)$,所以$\cos x - 1\in(-2,0)$,即$y'<0$,所以函数$y = \sin x - x + 1$在$(0,\pi)$上单调递减.故选B.
方法总结判断函数$y = f(x)$的单调性的步骤
第一步,确定函数的定义域;
第二步,求导数$f'(x)$的零点;
第三步,用$f'(x)$的零点将$f(x)$的定义域划分为若干个区间,列表给出$f'(x)$在各区间上的正负,由此得出函数$y = f(x)$在定义域上的单调性.
方法总结判断函数$y = f(x)$的单调性的步骤
第一步,确定函数的定义域;
第二步,求导数$f'(x)$的零点;
第三步,用$f'(x)$的零点将$f(x)$的定义域划分为若干个区间,列表给出$f'(x)$在各区间上的正负,由此得出函数$y = f(x)$在定义域上的单调性.
3. (多选)[2023·河北武安第三中学高二阶段练习]
已知函数$f(x)=(x^{2}-5x+7)e^{x}$,则函数$f(x)$在
下列区间上单调递增的有(
A. $(-\infty,1)$
B. $(1,2)$
C. $(2,+\infty)$
D. $(1,+\infty)$
已知函数$f(x)=(x^{2}-5x+7)e^{x}$,则函数$f(x)$在
下列区间上单调递增的有(
AC
)A. $(-\infty,1)$
B. $(1,2)$
C. $(2,+\infty)$
D. $(1,+\infty)$
答案:
3.AC【解析】由题意得$f(x)$的定义域为$\mathbf{R},f'(x)=(2x - 5 + x^2 - 5x + 7)e^x=(x^2 - 3x + 2)e^x=(x - 1)(x - 2)e^x$.所以当$x<1$时,$f'(x)>0$;当$1<x<2$时,$f'(x)<0$.所以$f(x)$在区间$(-\infty,1),(2,+\infty)$上单调递增(单调区间由两部分构成时,一定不要写成并集形式),在$(1,2)$上单调递减.故选AC.
4. [2023·陕西宝鸡渭滨高二期末]函数$f(x)=(x-3)e^{x}$的单调递减区间是
(
A.$(-\infty,-2)$
B.$(2,+\infty)$
C.$(-\infty,2)$
D.$(-2,+\infty)$
(
C
)A.$(-\infty,-2)$
B.$(2,+\infty)$
C.$(-\infty,2)$
D.$(-2,+\infty)$
答案:
4.C【解析】由题意得$f'(x)=(x - 2)e^x$.令$f'(x)=(x - 2)· e^x<0$(若$f'(x)>0$,则函数$f(x)$单调递增;若$f'(x)<0$,则函数$f(x)$单调递减),则$x<2$,所以函数$f(x)$的单调递减区间是$(-\infty,2)$.故选C.
5. [2023·湖北武汉高二联考]函数$y=\frac{1}{2}x^{2}-\ln x+2$
的单调递增区间为
(
A.$(-1,1)$
B.$(0,1)$
C.$[1,+\infty)$
D.$(0,+\infty)$
的单调递增区间为
(
C
)A.$(-1,1)$
B.$(0,1)$
C.$[1,+\infty)$
D.$(0,+\infty)$
答案:
5.C【解析】由题意得,函数的定义域为$\{x|x>0\}$(先求函数的定义域),$y' = x - \frac{1}{x}=\frac{x^2 - 1}{x}$.令$y'\geq0$,得$x\leq - 1$(舍去)或$x\geq1$.所以函数的单调递增区间为$[1,+\infty)$.故选C.
6. [2023·江苏南京大学附属中学高二期末改编]已
知函数$f(x)=\frac{1}{2}x^{2}-\left(a+\frac{1}{a}\right)x+\ln x$,其中$a>0$.试讨
论函数$f(x)$的单调区间.
知函数$f(x)=\frac{1}{2}x^{2}-\left(a+\frac{1}{a}\right)x+\ln x$,其中$a>0$.试讨
论函数$f(x)$的单调区间.
答案:
6.思维思路求函数$f(x)$的导函数→得到导函数的零点→讨论$a$的取值范围→由导函数的零点对函数的定义域分段→利用导函数在各区间内的符号判断原函数的单调性.
【解】由题意,得$f'(x)=x - \left(a + \frac{1}{a}\right) + \frac{1}{x}=\frac{(x - a)\left(x - \frac{1}{a}\right)}{x}(x>0)$.
令$f'(x)=0$,解得$x = a$或$x=\frac{1}{a}$.
①若$a<\frac{1}{a}$,则$0<a<1$,所以当$x$变化时,$f'(x),f(x)$的变化情况如下表.
$x$ $(0,a)$ $a$ $\left(a,\frac{1}{a}\right)$ $\frac{1}{a}$ $\left(\frac{1}{a},+\infty\right)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $\frac{1}{2}a^2 + \ln a - 1$ 单调递减 $\frac{1}{2a^2} + \ln a - 1$ 单调递增
由表知,$f(x)$的单调递增区间为$(0,a)$和$\left(\frac{1}{a},+\infty\right)$,单调递减区间为$\left(a,\frac{1}{a}\right)$.
②若$\frac{1}{a}<a$,则$a>1$,所以当$x$变化时,$f'(x),f(x)$的变化情况如下表.
$x$ $\left(0,\frac{1}{a}\right)$ $\frac{1}{a}$ $\left(\frac{1}{a},a\right)$ $a$ $(a,+\infty)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $\frac{1}{2a^2} + \ln a - 1$ 单调递减 $\frac{1}{2}a^2 + \ln a - 1$ 单调递增
由表知,$f(x)$的单调递增区间为$\left(0,\frac{1}{a}\right)$和$(a,+\infty)$,单调递减区间为$\left(\frac{1}{a},a\right)$;当$a = 1$时,函数$f(x)$的单调递增区间为$(0,+\infty)$.
综上所述,当$0<a<1$时,$f(x)$的单调递增区间为$(0,a)$和$\left(\frac{1}{a},+\infty\right)$,单调递减区间为$\left(a,\frac{1}{a}\right)$;当$a>1$时,$f(x)$的单调递增区间为$\left(0,\frac{1}{a}\right)$和$(a,+\infty)$,单调递减区间为$\left(\frac{1}{a},a\right)$;当$a = 1$时,函数$f(x)$的单调递增区间为$(0,+\infty)$.
【解】由题意,得$f'(x)=x - \left(a + \frac{1}{a}\right) + \frac{1}{x}=\frac{(x - a)\left(x - \frac{1}{a}\right)}{x}(x>0)$.
令$f'(x)=0$,解得$x = a$或$x=\frac{1}{a}$.
①若$a<\frac{1}{a}$,则$0<a<1$,所以当$x$变化时,$f'(x),f(x)$的变化情况如下表.
$x$ $(0,a)$ $a$ $\left(a,\frac{1}{a}\right)$ $\frac{1}{a}$ $\left(\frac{1}{a},+\infty\right)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $\frac{1}{2}a^2 + \ln a - 1$ 单调递减 $\frac{1}{2a^2} + \ln a - 1$ 单调递增
由表知,$f(x)$的单调递增区间为$(0,a)$和$\left(\frac{1}{a},+\infty\right)$,单调递减区间为$\left(a,\frac{1}{a}\right)$.
②若$\frac{1}{a}<a$,则$a>1$,所以当$x$变化时,$f'(x),f(x)$的变化情况如下表.
$x$ $\left(0,\frac{1}{a}\right)$ $\frac{1}{a}$ $\left(\frac{1}{a},a\right)$ $a$ $(a,+\infty)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 $\frac{1}{2a^2} + \ln a - 1$ 单调递减 $\frac{1}{2}a^2 + \ln a - 1$ 单调递增
由表知,$f(x)$的单调递增区间为$\left(0,\frac{1}{a}\right)$和$(a,+\infty)$,单调递减区间为$\left(\frac{1}{a},a\right)$;当$a = 1$时,函数$f(x)$的单调递增区间为$(0,+\infty)$.
综上所述,当$0<a<1$时,$f(x)$的单调递增区间为$(0,a)$和$\left(\frac{1}{a},+\infty\right)$,单调递减区间为$\left(a,\frac{1}{a}\right)$;当$a>1$时,$f(x)$的单调递增区间为$\left(0,\frac{1}{a}\right)$和$(a,+\infty)$,单调递减区间为$\left(\frac{1}{a},a\right)$;当$a = 1$时,函数$f(x)$的单调递增区间为$(0,+\infty)$.
7. [2023·广东深圳宝安第一外国语学校高二期中]函数$y=f(x)$的部分图像如图,
则(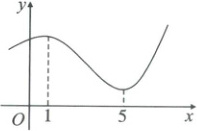
A.$f'(2)>0$
B.$f'(6)<0$
C.$f'(3)=0$
D.$f'(3)<0$
则(
D
)
A.$f'(2)>0$
B.$f'(6)<0$
C.$f'(3)=0$
D.$f'(3)<0$
答案:
7.D思维思路观察函数图像→得函数的单调性结合导数与函数的单调性的关系→判断导数值的符号.
【解析】由题图得$f(x)$在$[1,5]$上单调递减,在$(5,+\infty)$上单调递增,所以$f'(2)<0,f'(3)<0,f'(6)>0$.故选D.
【解析】由题图得$f(x)$在$[1,5]$上单调递减,在$(5,+\infty)$上单调递增,所以$f'(2)<0,f'(3)<0,f'(6)>0$.故选D.
8. [2023·陕西西安周至第六中学高
二期末]函数$y=f(x)$的图像
如图,则导函数$y=f'(x)$的图像
可能是(


二期末]函数$y=f(x)$的图像
如图,则导函数$y=f'(x)$的图像
可能是(
A
)

答案:
8.A【解析】由题图知$f(x)$为偶函数,则$f(x)=f(-x)$.因为$f(x)$的导数存在,所以两边取导数得$f'(x)=[f(-x)]'$.又$[f(-x)]'=f'(-x)·(-x)'=-f'(-x)$(复合函数求导法则应用),所以$f'(x)=-f'(-x)$,所以$f'(x)$为奇函数,排除C,D.由原函数的图像可知,当$x>0$时,$f(x)$先单调递增,再单调递减,故当$x>0$时,导函数$f'(x)$的值先正后负,排除B.故选A.
查看更多完整答案,请扫码查看


