《2025年练习生高中数学选择性必修第二册人教版》

1.[2023·浙江杭州学军中学高二月考]在等差数列$\{ a_{n}\}$中，$a_{1}=3$，且$a_{1},a_{4},a_{10}$成等比数列，则数列$\{ a_{n}\}$的通项公式为 (D)

A.$a_{n}=2n+1$
B.$a_{n}=n+2$
C.$a_{n}=2n+1$或$a_{n}=3$
D.$a_{n}=n+2$或$a_{n}=3$

答案： 1.D【解析】设等差数列$\{ a_{n}\}$的公差为$d$.因为$a_{1},a_{4},a_{10}$成等比数列，所以$a_{4}^{2}=a_{1}a_{10}$，则$(3 + 3d)^{2}=3×(3 + 9d)$，解得$d = 1$或$d = 0$，所以$a_{n}=a_{1}+(n - 1)d = n + 2$或$a_{n}=3$.故选D.

2.数列$\frac{3}{4},\frac{4}{7},\frac{5}{10}$,⋯的一个通项公式为 (A)

A.$a_{n}=\frac{n+2}{3n+1}$
B.$a_{n}=\frac{2n+1}{n+3}$
C.$a_{n}=\frac{n+2}{2n+2}$
D.$a_{n}=\frac{n+5}{5n+3}$

答案： 2.A【解析】因为数列的前三项分别为$\frac{3}{4},\frac{4}{7},\frac{5}{10}$，所以分子是首项为$3$，公差为$1$的等差数列，分母是首项为$4$，公差为$3$的等差数列，所以该数列的一个通项公式为$a_{n}=\frac{n + 2}{3n + 1}$.故选A.

3.已知数列$\{ a_{n}\}$中，$a_{1}=1,\frac{a_{n}-a_{n + 1}}{a_{n + 1}a_{n}}=1(n\in \mathbf{N}^{*}).$若$a_{m}=\frac{1}{10}$,则$m=$ (C)

A.8
B.9
C.10
D.11

答案： 3.C【解析】依题意，$n\in N^{*},\frac{a_{n}-a_{n + 1}}{a_{n + 1}a_{n}}=\frac{1}{a_{n + 1}}-\frac{1}{a_{n}} = 1$.又$\frac{1}{a_{1}} = 1$，所以数列$\{\frac{1}{a_{n}}\}$是以$1$为首项，$1$为公差的等差数列，所以$\frac{1}{a_{n}} = 1+(n - 1)×1 = n$，即$a_{n}=\frac{1}{n}$.由$a_{m}=\frac{1}{m}=\frac{1}{10}$，得$m = 10$.故选C.

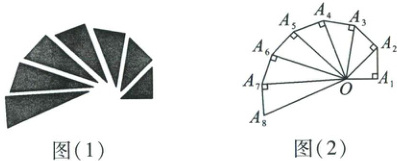
4.[2023·江苏连云港高二期末]如图(1)是第七届国际数学教育大会(简称 ICME-7)的会徽图案，会徽的主体图案是由如图(2)所示的一连串直角三角形演化而成的，其中$OA_{1} = A_{1}A_{2} = A_{2}A_{3} = ·s = A_{7}A_{8} = 1$，若把图(2)中的直角三角形继续作下去，记$OA_{1},OA_{2}, ·s ,OA_{n}, ·s$的长度构成数列$\{ a_{n}\}$，则此数列的通项公式为 (C)

A.$a_{n}=n$
B.$a_{n}=\sqrt{n + 1}$
C.$a_{n}=\sqrt{n}$
D.$a_{n}=n^{2}$

答案： 4.C思维路径根据所给的直角三角形中的边长关系结合勾股定理连续两项之间的关系$\to\{ a_{n}^{2}\}$是以$1$为首项，$1$为公差的等差数列写出通项得到结果.
【解析】根据题意得，$OA_{1}=A_{1}A_{2}=A_{2}A_{3}=·s=A_{7}A_{8}=1$，$\therefore a_{1}^{2}=a_{2}^{2}-1,\therefore\{ a_{n}^{2}\}$是以$1$为首项，$1$为公差的等差数列，$\therefore a_{n}^{2}=n,\therefore a_{n}=\sqrt{n}$.故选C.

5.已知数列$\{ a_{n}\}$满足$a_{n} + a_{n + 1} = 2n + 1(n\in \mathbf{N}^{*} ),a_{1} = 1$，则数列$\{ a_{n}\}$的通项公式为$a_{n} =$$n$.

答案： 5.$n$思维路径当$n\geq2$时，把$n$变为$n - 1\to a_{n - 1}+a_{n}=2(n - 1)+1 = 2n - 1$和原式相减$\to a_{n + 1}-a_{n - 1}=2\to$奇数项成等差数列，偶数项也成等差数列，公差均为$2\to$得解.
【解析】当$n\geq2$时，把$n$变为$n - 1$，得$a_{n - 1}+a_{n}=2(n - 1)+1 = 2n - 1$，和原式相减，得$a_{n + 1}-a_{n - 1}=2$，所以该数列的奇数项成等差数列，偶数项也成等差数列，公差均为$2$.由$a_{1}=1$得到奇数项$a_{n}=n$，把$n = 1$代入$a_{n}+a_{n + 1}=2n + 1$，解得$a_{2}=2$，所以偶数项$a_{n}=n$，从而$a_{n}=n$.

6.在数列$\{ a_{n}\}$中，$a_{1} = 1,a_{n + 1} = 2n - a_{n}$，则数列$\{ a_{n}\}$的通项公式为$a_{n} =$.

答案： 6.$\begin{cases}n,n为\\奇数,\\n-1,n\\为偶数\end{cases}$【解析】$\because a_{n + 1}=2n - a_{n},\therefore a_{n + 1}+a_{n}=2n$①，
$\because a_{1}=1,\therefore$数列$\{ a_{n}\}$的奇数项是首项为$1$，公差为$2$的等差数列，$\therefore$当$n$为奇数时，$a_{n}=n.\because$当$n$为偶数时，$n - 1$为奇数，$\therefore a_{n}=2(n - 1)-a_{n - 1}=2(n - 1)-(n - 1)=n - 1$，
$\therefore a_{n}=\begin{cases}n,n为\\奇数,\\n-1,n\\为偶数\end{cases}$.

7.在数列$\{ a_{n}\}$中，$a_{n + 1} - a_{n} = 3n - 22,a_{1} = - 2$，则$a_{30} =$ (D)

A.659
B.661
C.663
D.665

答案： 7.D【解析】因为$a_{n + 1}-a_{n}=3n - 22$，所以$a_{2}-a_{1}=-19,a_{3}-a_{2}=-16,·s,a_{30}-a_{29}=65$，累加得$a_{30}-a_{1}=\frac{(-19 + 65)×29}{2}=667$，所以$a_{30}=a_{1}+667 = 665$.故选D.

8.已知数列$\{ a_{n}\}$满足$a_{1} = 1,a_{2} = 2,a_{n + 2} - 2a_{n + 1} + a_{n} = \frac{1}{2}$，则$a_{100} =$
(C)

A.$\frac{5049}{2}$
B.2 525
C.$\frac{5051}{2}$
D.2 526

答案： 8.C【解析】由已知条件得$(a_{n + 2}-a_{n + 1})-(a_{n + 1}-a_{n})=\frac{1}{2}$，$\therefore$数列$\{ a_{n + 1}-a_{n}\}$为等差数列，$\therefore a_{n + 1}-a_{n}=(a_{2}-a_{1})+\frac{1}{2}(n - 1)=\frac{n + 1}{2}$，$\therefore$当$n\geq2$时，$a_{n}-a_{n - 1}=\frac{n}{2},·s,a_{3}-a_{2}=\frac{3}{2},a_{2}-a_{1}=\frac{2}{2}$
$\therefore(a_{n}-a_{n - 1})+·s+(a_{3}-a_{2})+(a_{2}-a_{1})=\frac{1}{2}(2 + 3+·s+n)(n\geq2)$(利用累加法求解)，$\therefore a_{n}=\frac{n^{2}+n + 2}{4}(n\geq2),\therefore a_{100}=\frac{5051}{2}$.故选C.

9.已知数列$\{ a_{n}\}$满足$a_{1} = 1,na_{n + 1} = (n + 1)a_{n} + 1$,令$b_{n} = \frac{a_{n}}{n}$.若对于任意$n\in \mathbf{N}^{*}$，不等式$b_{n + 1} ＜ 4 - 2^{t}$恒成立，则实数$t$的取值范围为 (D)

A.$\left ( - \infty, - \frac{3}{2} \right\rbrack$
B.$( - \infty , - 1\rbrack$
C.$( - \infty ,0\rbrack$
D.$( - \infty ,1\rbrack$

答案： 9.D思维路径根据题意，整理得$\frac{a_{n + 1}}{n + 1}=\frac{a_{n}}{n}+\frac{1}{n}-\frac{1}{n + 1}\to$利用累加法可得$b_{n + 1}=2-\frac{1}{n + 1}\to$结合题意可得$(b_{n + 1})_{max}＜4 - 2^{t}\to$运算求解.
【解析】$\because na_{n + 1}=(n + 1)a_{n}+1,\therefore\frac{a_{n + 1}}{n + 1}=\frac{a_{n}}{n}+\frac{1}{n(n + 1)}=\frac{a_{n}}{n}+\frac{1}{n}-\frac{1}{n + 1}$，即$b_{n + 1}-b_{n}=\frac{1}{n}-\frac{1}{n + 1}$.又$\because b_{n + 1}=(b_{n + 1}-b_{n})+(b_{n}-b_{n - 1})+·s+(b_{2}-b_{1})+b_{1},\therefore b_{n + 1}=\left(\frac{1}{n}-\frac{1}{n + 1}\right)+\left(\frac{1}{n - 1}-\frac{1}{n}\right)+·s+\left(1-\frac{1}{2}\right)+1 = 2-\frac{1}{n + 1}＜2$.由题意，得$2\leq4 - 2^{t},\therefore2^{t}\leq2,\therefore t\leq1$.
1.故选D.

10.已知数列$\{ a_{n}\}$满足$a_{1} = 1,a_{2} = \frac{1}{3},a_{n} \neq 0$，且$2a_{n + 1}a_{n}a_{n - 1} = a_{n + 1}a_{n} + a_{n}a_{n - 1} - 2a_{n + 1}a_{n - 1},n \geqslant 2$，则数列$\{ a_{n}\}$的通项公式为$a_{n} =$$\frac{1}{n^{2}-n+1}$.

答案： 10.$\frac{1}{n^{2}-n+1}$思维路径化简题设条件得到$\left(\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}\right)\left(\frac{1}{a_{n + 1}}-\frac{1}{a_{n - 1}}\right)=2\to$得出数列$\left\{\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}\right\}$是以$2$为首项，$2$为公差的等差数列得出$\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}$利用累加法得到答案.
【解析】因为$2a_{n + 1}a_{n - 1}=a_{n + 1}a_{n}+a_{n}a_{n - 1}-2a_{n + 1}a_{n - 1},n\geq2$，
等式两侧同时除以$a_{n + 1}a_{n}a_{n - 1}$，得$2=\frac{1}{a_{n - 1}}-\frac{1}{a_{n + 1}}+\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}$，即
$\left(\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}\right)-\left(\frac{1}{a_{n}}-\frac{1}{a_{n - 1}}\right)=2$，所以数列$\left\{\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}\right\}$是以$2$
为首项，$2$为公差的等差数列，则$\frac{1}{a_{n + 1}}-\frac{1}{a_{n}}=2+(n - 1)×2 = 2n$，所以$\frac{1}{a_{n}}=\frac{1}{a_{1}}+\left(\frac{1}{a_{2}}-\frac{1}{a_{1}}\right)+\left(\frac{1}{a_{3}}-\frac{1}{a_{2}}\right)+·s+\left(\frac{1}{a_{n}}-\frac{1}{a_{n - 1}}\right)=1+[2 + 4+·s+2(n - 1)]=1+\frac{(2 + 2n - 2)(n - 1)}{2}=n^{2}-n + 1(n\geq2)$.当$n = 1$时，$\frac{1}{a_{1}} = 1$也符合上式，所以$\frac{1}{a_{n}}=n^{2}-n + 1$，所以数列$\{ a_{n}\}$的通项公式为$a_{n}=\frac{1}{n^{2}-n + 1}$.