《2025年练习生高中数学选择性必修第二册人教版》

19. 若函数$f(x)=\frac{2}{3}x^{3}-2x^{2}+ax+10$在区间$[-1,4]$上
具有单调性，则实数$a$的取值范围是$(-\infty,-16]\cup[2,+\infty)$.

答案： 19.$(-\infty,-16]\cup[2,+\infty)$【解析】由题意得$f'(x)=2x^2 - 4x + a$,函数$f(x)$在区间$[-1,4]$上具有单调性等价于$f'(x)=2x^2 - 4x + a\leq0$或$f'(x)=2x^2 - 4x + a\geq0$在$[-1,4]$上恒成立,则当$x\in[-1,4]$时,$a\leq(-2x^2 + 4x)_{\min}$或$a\geq(-2x^2 + 4x)_{\max}$,即$a\leq - 16$或$a\geq2$.
易错规避本题中,由于函数在$[-1,4]$上具有单调性,因此应分函数在该区间上单调递增或单调递减两种情况讨论.另外,求解本题时应注意“函数在某一区间内$f'(x)＞0[$或$f'(x)＜0]$”是“函数在该区间上单调递增(或递减)”的充分不必要条件.若函数在该区间上单调递增(或减),则可以得到$f'(x)\geq0[$或$f'(x)\leq0]$在该区间上恒成立.

20. 已知函数$f(x)=\frac{1}{3}ax^{3}+x^{2}+x+4$，则“$a\geqslant0$”是
“$f(x)$在$\mathbf{R}$上单调递增”的(C)
A. 充要条件
B. 充分不必要条件
C. 必要不充分条件
D. 既不充分也不必要条件

答案： 20.C【解析】由题意得$f'(x)=ax^2 + 2x + 1$.若$f(x)$在$\mathbf{R}$上单调递增,则$f'(x)\geq0$在$\mathbf{R}$上恒成立,所以$\begin{cases}a＞0,\\\Delta = 4 - 4a\leq0,\end{cases}$解得$a\geq1$.故“$a\geq0$”是“$f(x)$在$\mathbf{R}$上单调递增”的必要不充分条件.选C.

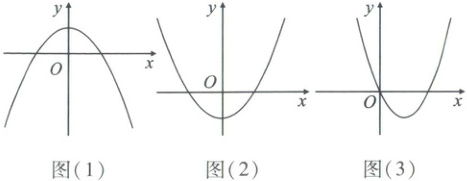
21. 如图(1)(2)(3)，有一个图像是函数$f(x)=\frac{1}{3}x^{3}+ax^{2}+(a^{2}-1)x+1(a\in\mathbf{R}$，且$a\neq0)$的导函数
的图像，则$f(-1)=$
(B)

A.$\frac{1}{3}$
B.$-\frac{1}{3}$
C.$\frac{7}{3}$
D.$-\frac{1}{3}$或$\frac{5}{3}$

答案： 21.B【解析】由题意得$f'(x)=x^2 + 2ax + a^2 - 1=[x + (a + 1)][x + (a - 1)]$.题图
(1)与题图
(2)中,导函数的图像的对称轴都是$y$轴,此时$a = 0$,与题意不符,故题图
(3)中的图像是函数$f(x)$的导函数的图像.由题图
(3)知$f'(0)=0$,所以$(a + 1)(a - 1)=0$,解得$a = 1$或$a = - 1$.由题图
(3)知,令方程$f'(x)=0$,得另一根为正数,故$a = - 1$.所以$f(x)=\frac{1}{3}x^3 - x^2 + 1$,所以$f(-1)=-\frac{1}{3}$.故选B.

22. [2023·安徽宿州高二期中]已知函数$f(x)=\ln x-a\sin x$在区间$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上单调递增，则实数
$a$的取值范围是
(C)

A.$\left(-\infty,\frac{2\sqrt{3}}{\pi}\right]$
B.$\left(-\infty,\frac{4\sqrt{3}}{\pi}\right]$
C.$\left(-\infty,\frac{4\sqrt{2}}{\pi}\right]$
D.$\left[\frac{2\sqrt{3}}{\pi},+\infty\right)$

答案： 22.C【解析】由题意得$f'(x)=\frac{1}{x} - a\cos x$.因为函数$f(x)$在区间$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上单调递增,所以$f'(x)\geq0$在$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上恒成立,即$a\leq\frac{1}{x\cos x}$在$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上恒成立(分离参数进行转化).设$h(x)=\frac{1}{x\cos x}$,则$h'(x)=\frac{-\cos x + x\sin x}{(x\cos x)^2}$.设$g(x)=-\cos x + x\sin x$,则$g'(x)=2\sin x + x\cos x$.当$x\in\left[\frac{\pi}{6},\frac{\pi}{4}\right]$时,$g'(x)＞0$,所以$g(x)$在$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上单调递增.因为$g\left(\frac{\pi}{4}\right)=-\cos\frac{\pi}{4}+\frac{\pi}{4}\sin\frac{\pi}{4}=\frac{\sqrt{2}}{2}+\frac{\pi}{4}×\frac{\sqrt{2}}{2}＜0$,所以在$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上,$h'(x)＜0$,所以$h(x)$在$\left[\frac{\pi}{6},\frac{\pi}{4}\right]$上单调递减,所以$a\leq h\left(\frac{\pi}{4}\right)=\frac{4\sqrt{2}}{\pi}$.故选C.

23. 为了激发同学们学习数学的
热情，某学校开展利用数学知
识设计 LOGO 的比赛，其中某
位同学利用函数图像的一部分设计了如图的
LOGO，那么该同学所选的函数最有可能的是
(B)

A.$f(x)=x-\sin x$
B.$f(x)=\sin x-x\cos x$
C.$f(x)=x^{2}-\frac{1}{x^{2}}$
D.$f(x)=\sin x+x^{3}$

答案： 23.B【解析】对于A,$f'(x)=1 - \cos x\geq0$,所以函数$f(x)$在定义域上单调递增,与题图不符.对于B,$f'(x)=\cos x - (\cos x - x\sin x)=x\sin x$.当$x\in(-2\pi,-\pi)$时,$f'(x)＜0$;当$x\in(-\pi,\pi)$时,$f'(x)＞0$;当$x\in(\pi,2\pi)$时,$f'(x)＜0$.所以$f(x)$在$(-2\pi,-\pi),(\pi,2\pi)$上单调递减,在$(-\pi,\pi)$上单调递增,与题图符合.对于C,由$f(-x)=(-x)^2 - \frac{1}{(-x)^2}=x^2 - \frac{1}{x^2}=f(x)$且定义域为$\{x|x\neq0\}$,知函数$f(x)$为偶函数.而题图中的图像不可能在$y$轴两侧,所以研究函数$f(x)$在$(0,+\infty)$上的性质:因为$f'(x)=2x + \frac{2}{x^3}＞0$,所以$f(x)$在$(0,+\infty)$上单调递增,与题图不符.对于D,由$f(-x)=\sin(-x)+(-x)^3=-\sin x - x^3=-f(x)$且定义域为$\mathbf{R}$,知函数$f(x)$为奇函数.研究函数$f(x)$在$(0,+\infty)$上的性质:因为$f'(x)=\cos x + 3x^2＞0$,所以$f(x)$在$\mathbf{R}$上单调递增,与题图不符.故选B.

24. 已知函数$f(x)$的导函数$f'(x)$满足：对任意的
$x\in\mathbf{R}$都有$f'(x)＞x$，若$f(1-k)-f(1+k)\geqslant-2k$，则
实数$k$的取值范围是(A)

A.$(-\infty,0]$
B.$\left(-\infty,\frac{1}{2}\right]$
C.$\left(0,\frac{1}{2}\right)$
D.$[0,+\infty)$

答案： 24.A思维思路$f'(x)＞x$→构造$F(x)=f(x)-\frac{1}{2}x^2$→得$F(x)$的单调性→对不等式变形后得到$F(1 - k)\geq F(1 + k)$→由函数的单调性解不等式.
【解析】设$F(x)=f(x)-\frac{1}{2}x^2$,则$F'(x)=f'(x)-x＞0$在$\mathbf{R}$上恒成立,所以$F(x)=f(x)-\frac{1}{2}x^2$在$\mathbf{R}$上单调递增.不等式$f(1 - k)-f(1 + k)\geq - 2k$可变形为$f(1 - k)-\frac{1}{2}(1 - k)^2\geq f(1 + k)-\frac{1}{2}(1 + k)^2$,即$F(1 - k)\geq F(1 + k)$,所以$1 - k\geq1 + k$,解得$k\leq0$.故选A.

25. 已知函数$f(x)$的图像关于点$(2,0)$对称，且当$x＞2$时，$f(x)$和其导函数$f'(x)$的单调性相反，请写
出$f(x)$的一个解析式：$f(x)=\frac{1}{x-2}(答案不唯一)$.

答案： 25.$f(x)=\frac{1}{x - 2}(答案不唯一)$【解析】由$f(x)$的图像关于点$(2,0)$对称,可设$f(x)=\frac{1}{x - 2}$,则$f'(x)=-\frac{1}{(x - 2)^2}$.当$x＞2$时,$f(x)$单调递减,$f'(x)$单调递增,满足题意.本题答案不唯一,其他满足条件的解析式也可以.

26. [2023·湖南娄底新化高二期末]已知函数$f(x)=2023^{x}+\frac{1}{2023^{x}}-\frac{1}{x^{2}+3}$，则不等式$f(x+1)＞f(2x)$的
解集为$\left(-\frac{1}{3},1\right)$.

答案： 26.$\left(-\frac{1}{3},1\right)$思维思路分析$f(x)$的奇偶性→对函数$f(x)$进行求导→判断函数$f(x)$的单调性→根据其单调性列出关于$x$的不等式求解即可.
【解析】由题意知,函数$f(x)$的定义域为$\mathbf{R}$,且$f(-x)=f(x)$,所以函数$f(x)$为偶函数.因为当$x\geq0$时,$f'(x)=2023^{-x}+\frac{1}{2023^{-x}}+\frac{2x}{(x^2 + 3)^2}\geq0$,又因为$f'(x)$不恒为零,所以函数$f(x)$在$[0,+\infty)$上为增函数.因为$f(|x + 1|)＞f(|2x|)$,所以$|x + 1|＞|2x|$,整理得$(3x + 1)(x - 1)＜0$,解得$-\frac{1}{3}＜x＜1$.
方法总结利用导数与函数的关系解不等式的步骤
第一步,根据函数的解析式判断函数的奇偶性;
第二步,求导或者直接观察判断函数在$(0,+\infty)$上的单调性;
第三步,根据函数的单调性和奇偶性列出不等式求解.

27. 设$a=\mathrm{e}^{\frac{1}{10}}·\mathrm{e}^{\frac{1}{9}},b=\frac{1}{9},c=2\ln\frac{3}{2}$，则c a b
$＞＞＞$
(填$a,b,c$)

答案： 27.c a b【解析】$a=\frac{1}{10}e^{\frac{1}{9}},b=\frac{1}{9}=\frac{1}{9}\left(1+\frac{1}{9}\right)$.设$f(x)=e^x - x - 1(x\geq0)$,则$f'(x)=e^x - 1\geq0$,当且仅当$x = 0$时取等号,所以函数$f(x)=e^x - x - 1$在$[0,+\infty)$上单调递增,所以$f\left(\frac{1}{9}\right)＞f(0)=0$,所以$\frac{1}{10}e^{\frac{1}{9}}＞\frac{1}{10}\left(1+\frac{1}{9}\right)$,故$a＞b$.因为$\left(\frac{3}{2}\right)^4=\frac{81}{16}＞e$,所以$\frac{3}{2}＞e^{\frac{1}{4}}$.因为函数$y=\ln x$在$(0,+\infty)$上单调递增,所以$\ln\frac{3}{2}＞\frac{1}{4}$,故$c = 2\ln\frac{3}{2}-\frac{1}{2}$.又$e＜2^2$,且函数$y = x^{\frac{1}{9}}$在$(0,+\infty)$上单调递增,所以$e^{\frac{1}{9}}＜2$,所以$a=\frac{1}{10}e^{\frac{1}{9}}＜2$,所以$a＜c$,所以$c＞a＞b$.