《2025年练习生高中数学选择性必修第二册人教版》

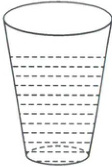
23. [2023·北京亦庄实验中学高一期末] 如图，向一个圆台形的容器倒水，任意相等时间间隔内所倒的水体积相等，记容器内水面的高度$h$随时间$t$变化的函数为$h = f(t)$，定义域为$D$，设$t_0 \in D$，$k_1$，$k_2$分别表示$f(t)$在区间$[t_0, t_0 + \Delta t]$，$[t_0 - \Delta t, t_0]$($\Delta t ＞ 0$)上的平均变化率，则 (A)

A.$k_1 ＜ k_2$
B.$k_1 ＞ k_2$
C.$k_1 = k_2$
D.无法确定

答案： 23.A 【解析】由容器的形状可知,在相同的时间间隔内,高度的增加量越来越小,所以$f(t)$在区间$[t_0 - \Delta t,t_0],[t_0,t_0 + \Delta t](\Delta t ＞ 0)$上的平均变化率由大变小（相同的时间间隔内,高度变化的快慢反映了平均变化率的大小）,即$k_2 ＞ k_1$.故选A.

24. (多选)[2023·山东聊城高二月考] 已知函数$f(x)$的图像如图，$f^\prime(x)$是$f(x)$的导函数，则下列结论正确的是 (BCD)

A.$f^\prime(3) ＞ f^\prime(2)$
B.$f^\prime(3) ＜ f^\prime(2)$
C.$f(3) - f(2) ＞ f^\prime(3)$
D.$f(3) - f(2) ＜ f^\prime(2)$

答案： 24.BCD 【解析】由题图可知,函数$f(x)$是单调递增的,所以函数$f(x)$在任意一点处的导函数值都大于零.又由题图知,函数$f(x)$的图像在$x = 2$处的切线斜率$k_1$大于其在$x = 3$处的切线斜率$k_2$,所以$f'(2) ＞ f'(3)$,故A错误,B正确.记$A(2,f(2)),B(3,f(3))$.连接$AB$,则直线$AB$的斜率$k = \frac{f(3) - f(2)}{3 - 2} = f(3) - f(2)$.由题图知$k_1 ＞ k ＞ k_2 ＞ 0$,即$f'(2) ＞ f(3) - f(2) ＞ f'(3) ＞ 0$,故C,D正确.选BCD.

25. [2023·湖北武汉部分重点中学高二期末] 2022年2月，第24届冬季奥林匹克运动会在北京隆重举行，中国代表团获得了“9金4银2铜”的优异成绩，彰显了我国体育强国的底蕴和综合国力. 设某高山滑雪运动员在一次滑雪训练中滑行的路程$l$(单位：$m$)与时间$t$(单位：$s$)之间的关系为$l(t) = 2t^2 + \frac{3}{2}t$，则当$t = 3 s$时，该运动员的滑雪瞬时变化率为$\frac{27}{2}$$m/s$.

答案： 25.$\frac{27}{2}$ 【解析】因为$l(3 + \Delta t) - l(3) = 2(3 + \Delta t)^2 + \frac{3}{2}(3 + \Delta t) - 2 × 3^2 - \frac{9}{2} = 2(\Delta t)^2 + \frac{27}{2}\Delta t$,所以当$t = 3s$时,该运动员的滑雪瞬时变化率（瞬时变化率也就是瞬时速度）为$l'(3) = \lim_{\Delta t \to 0} \frac{l(3 + \Delta t) - l(3)}{\Delta t} = \lim_{\Delta t \to 0} (2\Delta t + \frac{27}{2}) = \frac{27}{2}(m/s)$.

26. [2023·山西太原师范学院附属中学高二月考] 已知函数$f(x) = x^2 + 2x$在$[0, a]$上的平均变化率是函数$g(x) = 2x - 3$在$[2, 3]$上的平均变化率的$2$倍，则实数$a$的值为2；估计函数$f(x)$在$x = a$处的瞬时变化率为6.

答案： 26.$6$ 【解析】函数$f(x)$在$[0,a]$上的平均变化率为$\frac{f(a) - f(0)}{a - 0} = \frac{a^2 + 2a}{a} = a + 2$,函数$g(x)$在$[2,3]$上的平均变化率为$\frac{g(3) - g(2)}{3 - 2} = \frac{2 × 3 - 3 - (2 × 2 - 3)}{1} = 2$.由题意知$a + 2 = 2 × 2$,所以$a = 2$.函数$f(x)$在$[2,2 + \Delta x]$上的平均变化率为$\frac{(2 + \Delta x)^2 + 2(2 + \Delta x) - (2^2 + 2 × 2)}{\Delta x} = \frac{\Delta x^2 + 6\Delta x}{\Delta x} = \Delta x + 6$,则$\lim_{\Delta x \to 0} (\Delta x + 6) = 6$,故函数$f(x)$在$x = 2$处的瞬时变化率为$6$.

27. 已知函数$f(x) = x^3$.
(1) 求函数$f(x)$的导函数；
(2) 过点$P(\frac{2}{3}, 0)$作函数$f(x)$的图像的切线，求切线方程.

答案： 27.思维路径
(1)求函数$f(x)$在$[x,x + \Delta x]$上的平均变化率$\to$求当$\Delta x \to 0$时的极限.
(2)设切点为$Q(x_0,x_0^3) \to$根据导数的几何意义并利用直线方程的点斜式表示切线方程$\to$结合已知条件求得切点坐标$\to$即可得切线方程.
【解】
(1)因为$\frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) - f(x)}{\Delta x} = \frac{(x + \Delta x)^3 - x^3}{\Delta x} = \frac{x^3 + 3x^2 \Delta x + 3x(\Delta x)^2 + (\Delta x)^3 - x^3}{\Delta x} = 3x^2 + 3x \Delta x + (\Delta x)^2$,所以$\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} [3x(x + \Delta x) + (\Delta x)^2] = 3x^2$,所以函数$f(x)$的导函数$f'(x) = 3x^2$.
(2)设切点为$Q(x_0,x_0^3)$.由
(1)知切线斜率$k = f'(x_0) = 3x_0^2$,则切线方程为$y - x_0^3 = 3x_0^2(x - x_0)$,即$y = 3x_0^2x - 2x_0^3$.因为切线过点$P(\frac{2}{3},0)$,所以$2x_0^3 - 2x_0^3 = 0$,解得$x_0 = 0$或$x_0 = 1$.从而切线方程为$y = 0$或$y = 3x - 2$.

28. 生产某塑料管的利润函数为$P(n) = -n^3 + 600n^2 + 67\ 500n - 1\ 200\ 000$，其中$n$为工厂每月生产该塑料管的根数，利润$P(n)$的单位为元.
(1) 求边际利润函数$P^\prime(n)$；
(2) 求$n$的值，使$P^\prime(n) = 0$；
(3) 解释(2)中$n$的值的实际意义.

答案： 28.【解】
(1)因为$\frac{\Delta y}{\Delta n} = \frac{1}{ \Delta n} [ -(n + \Delta n)^3 + 600(n + \Delta n)^2 + 67500(n + \Delta n) - 1200000 - (-n^3 + 600n^2 + 67500n - 1200000)] = (-3n^2 + 1200n + 67500) - 3n \Delta n - (\Delta n)^2 - 3n \Delta n + 600 \Delta n$,所以$\lim_{\Delta n \to 0} \frac{\Delta y}{\Delta n} = -3n^2 + 1200n + 67500$,所以边际利润函数$P'(n) = -3n^2 + 1200n + 67500$.
(2)由题意并结合
(1),知$P'(n) = -3n^2 + 1200n + 67500 = 0,n \in \mathbf{N}^*$,整理,得$(n - 450)(n + 50) = 0$,解得$n = 450$(负值已舍去).
(3)由
(2)知$n = 450$,即每月生产该塑料管的根数为$450$时,工厂获得最大利润.