《2025年练习生高中数学选择性必修第二册人教版》

1.(多选)一球沿着某一斜面自由滚下，测得滚下的垂直距离$h$(单位：m)与时间$t$(单位：s)之间的函数关系为$h(t)=2t^{2}+2t$，则下列说法正确的是
(BCD)

A.前 3 s 内，球滚下的垂直距离的增量$\Delta h = 20$ m
B.在时间段$[2,3]$内，球滚下的垂直距离的增量$\Delta h = 12$ m
C.前 3 s 内，球在垂直方向上的平均速度为 8 m/s
D.在时间段$[2,3]$内，球在垂直方向上的平均速度为 12 m/s

答案： 1.BCD 【解析】前3s内，$\Delta t=3s$，$\Delta h=h(3)-h(0)=24m$，此时球在垂直方向上的平均速度为$\frac{\Delta h}{\Delta t}=\frac{24}{3}=8(m/s)$(根据前3s内的$\Delta t$，$\Delta h$可求得平均速度)，故A错误，C正确.在时间段$[2,3]$内，$\Delta t=1s$，$\Delta h=h(3)-h(2)=12m$，此时球在垂直方向上的平均速度为$\frac{\Delta h}{\Delta t}=\frac{12}{1}=12(m/s)$(根据在时间段$[2,3]$内的$\Delta t$，$\Delta h$可求得平均速度)，故B，D正确.选BCD.

2. 小球在光滑斜面上向下滚动，从开始滚动算起，时间$t$ s 内所经过的距离(单位：m)为$s(t)=at^{2}$，求小球在时间段$[2,2 + h]$内的平均速度.
题型 2 瞬时速度

答案： 2.【解】因为小球在时间$t$s内所经过的距离$s(t)=at^2$，所以在时间段$[2,2+h]$内的平均速度为$\frac{s(2+h)-s(2)}{2+h-2}=\frac{a(2+h)^2-a×2^2}{h}=4a+ah(m/s)$(求平均速度要确定时间的变化量$\Delta t$及距离的变化量$\Delta s$).

3. [2023·福建南平高二期末]如果质点$A$运动的位移$s$(单位：m)与时间$t$(单位：s)之间的函数关系为$s(t)=\frac{2}{t}$，那么该质点在$t = 3$ s 时的瞬时速度为
(D)

A.$\frac{2}{3}$ m/s
B.$-\frac{2}{3}$ m/s
C.$\frac{2}{9}$ m/s
D.$-\frac{2}{9}$ m/s

答案： 3.D 【解析】因为$\frac{\Delta s}{\Delta t}=\frac{s(3+\Delta t)-s(3)}{\Delta t}=\frac{3+\Delta t}{\Delta t}=\frac{2}{3(3+\Delta t)}$，所以$\lim_{\Delta t \to 0}\frac{\Delta s}{\Delta t}=\lim_{\Delta t \to 0}[\frac{2}{3(3+\Delta t)}]=-\frac{2}{9}$.故选D.
方法总结 求瞬时速度的步骤
第一步，求平均变化率$\frac{\Delta s}{\Delta t}$；
第二步，求$\Delta t \to 0$时$\frac{\Delta s}{\Delta t}$的值.

4. 在曲线$y = x^{2}$上取一点$(1,1)$及附近一点$(1+\Delta x,1+\Delta y)$，则曲线在点$(1,1)$处的切线的斜率为
(B)

A.$\Delta x+\frac{1}{\Delta x}+2$
B.2
C.$\Delta x + 2$
D.$2+\Delta x-\frac{1}{\Delta x}$

答案： 4.B 【解析】设$f(x)=x^2$，则$\lim_{\Delta x \to 0}\frac{f(1+\Delta x)-f(1)}{\Delta x}=\lim_{\Delta x \to 0}\frac{(1+\Delta x)^2-1^2}{\Delta x}=\lim_{\Delta x \to 0}(\Delta x+2)=2$.故选B.

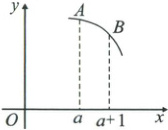
5. [2023·河南商丘名校高二联考]函数$f(x)$的图像如图，$k_{a}$为函数$f(x)$的图像在$x = a$处的切线斜率，$k_{b}$为函数$f(x)$的图像在$x = a + 1$处的切线斜率，下列排序正确的是
(C)


A.$f(a + 1)-f(a)＜k_{a}＜k_{b}$
B.$k_{b}＜k_{a}＜f(a + 1)-f(a)$
C.$k_{b}＜f(a + 1)-f(a)＜k_{a}$
D.$k_{a}＜f(a + 1)-f(a)＜k_{b}$

答案： 5.C 【解析】由题图可知$k_b＜k_a＜0$.又$f(a+1)-f(a)=\frac{f(a+1)-f(a)}{(a+1)-a}$(分母为1，注意将式子变形为直线斜率的形式)为割线AB的斜率，所以$k_b＜f(a+1)-f(a)＜k_a$.故选C.

6. 已知曲线$y = x^{2}-1$上两点$A(2,3)$，$B(2+\Delta x,3+\Delta y)$，当$\Delta x = 1$时，割线$AB$的斜率是5；当$\Delta x = 0.1$时，割线$AB$的斜率是4.1.

答案： 6.5 4.1 【解析】$\because \frac{\Delta y}{\Delta x}=\frac{(2+\Delta x)^2-1-(2^2-1)}{\Delta x}=\Delta x+4,\therefore$当$\Delta x=1$时，割线AB的斜率$k_1=5$；当$\Delta x=0.1$时，割线AB的斜率$k_2=4.1$.

7. 汽车行驶的路程$s$和时间$t$之间的函数如图，在时间段$[t_{0},t_{1}]$，$[t_{1},t_{2}]$，$[t_{2},t_{3}]$上的平均速度分别为$\bar{v}_{1}$，$\bar{v}_{2}$，$\bar{v}_{3}$，三者的大小关系为$\overline{v}_3＞\overline{v}_2＞\overline{v}_1$(从大到小排列).

答案：
7. $\overline{v}_3＞\overline{v}_2＞\overline{v}_1$ 【解析】如图，连接OA，AB，BC.根据题意，汽车在时间段$[t_0,t_1],[t_1,t_2],[t_2,t_3]$上的平均速度分别为$\overline{v}_1,\overline{v}_2,\overline{v}_3$，它们分别为直线OA,AB,BC的斜率.由图得$k_{BC}＞k_{AB}＞k_{OA}$，故$\overline{v}_3＞\overline{v}_2＞\overline{v}_1$.

易错规避 瞬时速度为函数图像在某点处的切线斜率，平均速度为函数图像在某区间上的割线斜率.如本题，连接OA,AB,BC，由割线斜率公式可得$\overline{v}_1,\overline{v}_2$，$\overline{v}_3$分别为直线OA,AB,BC的斜率.