《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

4. (多选)软木锅垫一般用于餐厅、咖啡厅、酒店等公共饮食场所，可作广告饰品以提高形象。杯垫透气、无毒、无异味、防水防潮、耐油耐酸、弹性环保，具有耐冲击、不变形、耐用等特点。正、反面可加置印刷公司$LOGO$、图片、产品、广告、联系方式等，更接近人们的生活，较强的摩擦力可以防止玻璃、瓷杯滑落，亦可保护桌面不被烫坏。如图，这是一个边长为10厘米的正六边形的软木锅垫$ABCDEF$,则下列选项正确的是


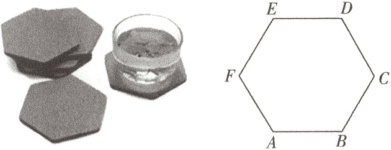
A.向量$\overrightarrow{AE}$与向量$\overrightarrow{BD}$是相等向量
B.$\overrightarrow{AB}·\overrightarrow{FE}=50\sqrt{3}$
C.$\overrightarrow{AD}·\overrightarrow{AB}=|\overrightarrow{AB}|^{2}$
D.$|\overrightarrow{AC}+\overrightarrow{AE}|=30$

答案：
4.ACD 由图可得向量$\overrightarrow{AE}$与向量$\overrightarrow{BD}$方向相同，大小相等，所以向量$\overrightarrow{AE}$与向量$\overrightarrow{BD}$相等向量，A正确；
由图易得向量$\overrightarrow{AB}$与向量$\overrightarrow{FE}$的夹角为$60^{\circ}$，则$\overrightarrow{AB}·\overrightarrow{FE}=10×10×\cos60^{\circ}=50$，B错误；
如图，因为$\angle FAB = 120^{\circ}$，$\angle DAB = 60^{\circ}$，$\overrightarrow{AD}·\overrightarrow{AB}=\vert\overrightarrow{AD}\vert·\vert\overrightarrow{AB}\vert·\cos60^{\circ}=\vert\overrightarrow{AB}\vert^{2}$，C正确；
因为$\triangle ACE$为正三角形，所以根据平行四边形法则得$\overrightarrow{AC}+\overrightarrow{AE}=2\overrightarrow{AH}$，
$\overrightarrow{AH}$与$\overrightarrow{AD}$共线且同方向，又$\triangle EDH$，$\triangle AEH$均为含$\frac{\pi}{6}$角的直角三角形，所以$\vert\overrightarrow{EH}\vert=\sqrt{3}\vert\overrightarrow{DH}\vert$，$\vert\overrightarrow{AH}\vert=\sqrt{3}\vert\overrightarrow{EH}\vert=3\vert\overrightarrow{DH}\vert$，$\vert\overrightarrow{AD}\vert=4\vert\overrightarrow{DH}\vert$，
所以$\frac{2\vert\overrightarrow{AH}\vert}{\vert\overrightarrow{AD}\vert}=\frac{3}{2}$，$\vert\overrightarrow{AC}+\overrightarrow{AE}\vert=\frac{3}{2}\vert\overrightarrow{AD}\vert=\frac{3}{2}×20 = 30$，D正确.
故选ACD.

5. 若非零向量$a,b$满足$|a|=3|b|=|a + 2b|$,则$a$与$b$夹角的余弦值为$-\frac{1}{3}$.

答案： 5.$-\frac{1}{3}$ $\because\vert a\vert = 3\vert b\vert=\vert a + 2b\vert$，
$\therefore\vert a\vert^{2}=9\vert b\vert^{2}=(a + 2b)^{2}=\vert a\vert^{2}+4\vert b\vert^{2}+4a· b$，
$\therefore a· b=-\vert b\vert^{2}$，
$\therefore\cos\langle a,b\rangle=\frac{a· b}{\vert a\vert\vert b\vert}=\frac{-\vert b\vert^{2}}{3\vert b\vert·\vert b\vert}=-\frac{1}{3}$.

6. 如图所示，已知圆$O$为$\triangle ABC$的外接圆，$AB=6,BC=7,CA=8$,则$\overrightarrow{OA}·\overrightarrow{AB}+\overrightarrow{OB}·\overrightarrow{BC}+\overrightarrow{OC}·\overrightarrow{CA}=$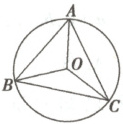$-\frac{149}{2}$.

答案： 6.$-\frac{149}{2}$ $\overrightarrow{OA}·\overrightarrow{AB}=\vert\overrightarrow{OA}\vert\vert\overrightarrow{AB}\vert\cos(180^{\circ}-\angle BAO)$，
$\because\vert\overrightarrow{OA}\vert\cos(180^{\circ}-\angle BAO)=-\vert\overrightarrow{OA}\vert\cos\angle BAO=-\frac{1}{2}\vert\overrightarrow{AB}\vert$，
$\therefore\overrightarrow{OA}·\overrightarrow{AB}=-\frac{1}{2}\vert\overrightarrow{AB}\vert^{2}$，
同理，$\overrightarrow{OB}·\overrightarrow{BC}=-\frac{1}{2}\vert\overrightarrow{BC}\vert^{2}$，$\overrightarrow{OC}·\overrightarrow{CA}=-\frac{1}{2}\vert\overrightarrow{CA}\vert^{2}$，
$\therefore\overrightarrow{OA}·\overrightarrow{AB}+\overrightarrow{OB}·\overrightarrow{BC}+\overrightarrow{OC}·\overrightarrow{CA}=-\frac{1}{2}×(6^{2}+7^{2}+8^{2})=-\frac{149}{2}$.

7. 已知$|m|=3,|n|=5,(3m + 2n)·(2m - n)=-2$.
(1)求$|m + n|$;
(2)求向量$m$在向量$m + n$方向上的投影向量的长度.

答案： 7.
(1)$\because(3m + 2n)·(2m - n)=-2$，
$\therefore6m^{2}+m· n - 2n^{2}=-2$，
$\because\vert m\vert = 3$，$\vert n\vert = 5$，$\therefore m· n=-6$.
$\therefore\vert m + n\vert=\sqrt{\vert m\vert^{2}+\vert n\vert^{2}+2m· n}=\sqrt{3^{2}+5^{2}+2×(-6)}=\sqrt{22}$.
(2)$\because m·(m + n)=m^{2}+m· n=9 - 6 = 3$，
$\therefore$向量$m$在向量$m + n$上的投影向量的长度为$\frac{m·(m + n)}{\vert m + n\vert}=\frac{3}{\sqrt{22}}=\frac{3\sqrt{22}}{22}$.

8. 在$\triangle ABC$中，角$A,B,C$所对的边长分别为$a,b,c$,以点$A$为圆心，$r$为半径作圆，如图所示，其中$PQ$为圆$A$的直径，试判断$P,Q$在什么位置时，$\overrightarrow{BP}·\overrightarrow{CQ}$有最大值.

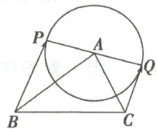
答案： 8.$\because\overrightarrow{BP}=\overrightarrow{AP}-\overrightarrow{AB}$，$\overrightarrow{CQ}=\overrightarrow{CA}-\overrightarrow{QA}=-\overrightarrow{AC}-\overrightarrow{AP}$，
$\therefore\overrightarrow{BP}·\overrightarrow{CQ}=(\overrightarrow{AP}-\overrightarrow{AB})·(-\overrightarrow{AC}-\overrightarrow{AP})=(-\overrightarrow{AP}·\overrightarrow{AC})+\overrightarrow{AB}·\overrightarrow{AC}-\overrightarrow{AP}^{2}+\overrightarrow{AB}·\overrightarrow{AP}=\overrightarrow{AB}·\overrightarrow{AC}-r^{2}+\overrightarrow{AP}·(\overrightarrow{AB}-\overrightarrow{AC})=\vert\overrightarrow{AB}\vert\vert\overrightarrow{AC}\vert\cos\angle BAC - r^{2}+\overrightarrow{AP}·\overrightarrow{CB}$.
当$\overrightarrow{AP}$与$\overrightarrow{CB}$同向时，$\overrightarrow{AP}·\overrightarrow{CB}$的最大值为$\vert\overrightarrow{AP}\vert\vert\overrightarrow{CB}\vert = ra$，
即当$QP$与$CB$共线且同向时，$\overrightarrow{BP}·\overrightarrow{CQ}$有最大值为$bc\cos\angle BAC + ar - r^{2}$.