2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5.已知向量$\boldsymbol{a}=(\sqrt{3},1)$,$\boldsymbol{b}=(0,-1)$,$\boldsymbol{c}=(k,\sqrt{3})$.若$\boldsymbol{a}-2\boldsymbol{b}$与$\boldsymbol{c}$共线,则$k =$
1
.
答案:
5.1 $\boldsymbol{a}-2\boldsymbol{b}=(\sqrt{3},3)$.因为$\boldsymbol{a}-2\boldsymbol{b}$与$\boldsymbol{c}$共线,
所以$\frac{k}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,解得$k = 1$.
所以$\frac{k}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,解得$k = 1$.
6.已知点$P_{1}(2,-1)$,点$P_{2}(-1,3)$,点$P$在线段$P_{1}P_{2}$上,且$\vert\overrightarrow{P_{1}P}\vert=\frac{2}{3}\vert\overrightarrow{PP_{2}}\vert$,则求点$P$的坐标为
$(\frac{4}{5},\frac{3}{5})$
.
答案:
6.$(\frac{4}{5},\frac{3}{5})$ 设点$P$的坐标为$(x,y)$,
由于点$P$在线段$P_1P_2$上,则有$\overrightarrow{P_1P}=\frac{2}{3}\overrightarrow{PP_2}$,
又$\overrightarrow{P_1P}=(x - 2,y + 1)$,$\overrightarrow{PP_2}=(-1 - x,3 - y)$,
由题意得$\begin{cases}x - 2=\frac{2}{3}(-1 - x),\\y + 1=\frac{2}{3}(3 - y),\end{cases}$解得$\begin{cases}x=\frac{4}{5},\\y=\frac{3}{5},\end{cases}$
$\therefore$点$P$的坐标为$(\frac{4}{5},\frac{3}{5})$.
由于点$P$在线段$P_1P_2$上,则有$\overrightarrow{P_1P}=\frac{2}{3}\overrightarrow{PP_2}$,
又$\overrightarrow{P_1P}=(x - 2,y + 1)$,$\overrightarrow{PP_2}=(-1 - x,3 - y)$,
由题意得$\begin{cases}x - 2=\frac{2}{3}(-1 - x),\\y + 1=\frac{2}{3}(3 - y),\end{cases}$解得$\begin{cases}x=\frac{4}{5},\\y=\frac{3}{5},\end{cases}$
$\therefore$点$P$的坐标为$(\frac{4}{5},\frac{3}{5})$.
7.如图,在边长为$1$的正方形$ABCD$中,$AB$与$x$轴正半轴成$30^{\circ}$角.求点$B$和点$D$的坐标和$\overrightarrow{AB}$与$\overrightarrow{AD}$的坐标.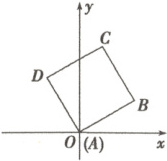

答案:
7.由题知$B,D$分别是$30^{\circ},120^{\circ}$角的终边与单位圆的交点.设
$B(x_1,y_1)$,$D(x_2,y_2)$.
由三角函数的定义,得
$x_1=\cos 30^{\circ}=\frac{\sqrt{3}}{2}$,$y_1=\sin 30^{\circ}=\frac{1}{2}$,
$\therefore B(\frac{\sqrt{3}}{2},\frac{1}{2})$.
$x_2=\cos 120^{\circ}=-\frac{1}{2}$,$y_2=\sin 120^{\circ}=\frac{\sqrt{3}}{2}$,
$\therefore D(-\frac{1}{2},\frac{\sqrt{3}}{2})$.
$\therefore \overrightarrow{AB}=(\frac{\sqrt{3}}{2},\frac{1}{2})$,$\overrightarrow{AD}=(-\frac{1}{2},\frac{\sqrt{3}}{2})$.
$B(x_1,y_1)$,$D(x_2,y_2)$.
由三角函数的定义,得
$x_1=\cos 30^{\circ}=\frac{\sqrt{3}}{2}$,$y_1=\sin 30^{\circ}=\frac{1}{2}$,
$\therefore B(\frac{\sqrt{3}}{2},\frac{1}{2})$.
$x_2=\cos 120^{\circ}=-\frac{1}{2}$,$y_2=\sin 120^{\circ}=\frac{\sqrt{3}}{2}$,
$\therefore D(-\frac{1}{2},\frac{\sqrt{3}}{2})$.
$\therefore \overrightarrow{AB}=(\frac{\sqrt{3}}{2},\frac{1}{2})$,$\overrightarrow{AD}=(-\frac{1}{2},\frac{\sqrt{3}}{2})$.
8.如图,已知直角梯形$ABCD$,$AD\perp AB$,$AB = 2AD = 2CD$,过点$C$作$CE\perp AB$于$E$,$M$为$CE$的中点,用向量的方法证明:
(1)$DE// BC$;
(2)$D$、$M$、$B$三点共线.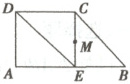
(1)$DE// BC$;
(2)$D$、$M$、$B$三点共线.

答案:
8.如图,以$E$为原点,$AB$所在直线为$x$轴,$EC$所在直线为$y$轴建立直角坐标系,令$|\overrightarrow{AD}| = 1$,则$|\overrightarrow{DC}| = 1$,$|\overrightarrow{AB}| = 2$.
$\because CE \perp AB$,而$AD = DC$,
$\therefore$四边形$AECD$为正方形.
可求得各点坐标分别为:$E(0,0)$,$B(1,0)$,$C(0,1)$,$D(-1,1)$,$A(-1,0)$.
(1)$\because \overrightarrow{ED}=(-1,1)-(0,0)=(-1,1)$,$\overrightarrow{BC}=(0,1)-(1,0)=(-1,1)$,
$\therefore \overrightarrow{ED}=\overrightarrow{BC}$,$\therefore \overrightarrow{ED} // \overrightarrow{BC}$,又$E,D,C,B$四点不共线,
$\therefore DE // BC$.
(2)$\because M$为$EC$的中点,$\therefore M(0,\frac{1}{2})$,
$\therefore \overrightarrow{MD}=(-1,1)-(0,\frac{1}{2})=(-1,\frac{1}{2})$,
$\overrightarrow{MB}=(1,0)-(0,\frac{1}{2})=(1,-\frac{1}{2})$.
$\therefore \overrightarrow{MD}=-\overrightarrow{MB}$,$\therefore \overrightarrow{MD} // \overrightarrow{MB}$.
又$MD$与$MB$共点于$M$,
$\therefore D,M,B$三点共线.

8.如图,以$E$为原点,$AB$所在直线为$x$轴,$EC$所在直线为$y$轴建立直角坐标系,令$|\overrightarrow{AD}| = 1$,则$|\overrightarrow{DC}| = 1$,$|\overrightarrow{AB}| = 2$.
$\because CE \perp AB$,而$AD = DC$,
$\therefore$四边形$AECD$为正方形.
可求得各点坐标分别为:$E(0,0)$,$B(1,0)$,$C(0,1)$,$D(-1,1)$,$A(-1,0)$.
(1)$\because \overrightarrow{ED}=(-1,1)-(0,0)=(-1,1)$,$\overrightarrow{BC}=(0,1)-(1,0)=(-1,1)$,
$\therefore \overrightarrow{ED}=\overrightarrow{BC}$,$\therefore \overrightarrow{ED} // \overrightarrow{BC}$,又$E,D,C,B$四点不共线,
$\therefore DE // BC$.
(2)$\because M$为$EC$的中点,$\therefore M(0,\frac{1}{2})$,
$\therefore \overrightarrow{MD}=(-1,1)-(0,\frac{1}{2})=(-1,\frac{1}{2})$,
$\overrightarrow{MB}=(1,0)-(0,\frac{1}{2})=(1,-\frac{1}{2})$.
$\therefore \overrightarrow{MD}=-\overrightarrow{MB}$,$\therefore \overrightarrow{MD} // \overrightarrow{MB}$.
又$MD$与$MB$共点于$M$,
$\therefore D,M,B$三点共线.

查看更多完整答案,请扫码查看


