2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知$|\overrightarrow{AB}| = 10,|\overrightarrow{AC}| = 7$,则$|\overrightarrow{BC}|$的取值范围是 (
A.$[3,17]$
B.$(3,17)$
C.$(3,10)$
D.$[3,10]$
A
)A.$[3,17]$
B.$(3,17)$
C.$(3,10)$
D.$[3,10]$
答案:
1.A 利用三角形两边之和大于第三边,两边之差小于第三边的性质及$\overrightarrow{AB}$与$\overrightarrow{AC}$共线时的情况求解.
即$|\overrightarrow{AB}|-|\overrightarrow{AC}|\leq|\overrightarrow{BC}|\leq|\overrightarrow{AC}|+|\overrightarrow{AB}|$,故$3\leq|\overrightarrow{BC}|\leq17$.
即$|\overrightarrow{AB}|-|\overrightarrow{AC}|\leq|\overrightarrow{BC}|\leq|\overrightarrow{AC}|+|\overrightarrow{AB}|$,故$3\leq|\overrightarrow{BC}|\leq17$.
2. 如图所示的方格纸中有定点$O,P,Q,E,F,G,H$,则$\overrightarrow{OP}+\overrightarrow{OQ} =$
(
A.$\overrightarrow{OH}$
B.$\overrightarrow{OG}$
C.$\overrightarrow{FO}$
D.$\overrightarrow{EO}$

(
C
)A.$\overrightarrow{OH}$
B.$\overrightarrow{OG}$
C.$\overrightarrow{FO}$
D.$\overrightarrow{EO}$
答案:
2.C $\overrightarrow{OP}+\overrightarrow{OQ}=\overrightarrow{FO}$.
3. 若$M$为$\triangle ABC$的重心,则下列各向量中与$\overrightarrow{AB}$共线的是 (
A.$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AC}$
B.$\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{BC}$
C.$\overrightarrow{AM}+\overrightarrow{BM}+\overrightarrow{CM}$
D.$3\overrightarrow{AM}+\overrightarrow{AC}$
C
)A.$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AC}$
B.$\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{BC}$
C.$\overrightarrow{AM}+\overrightarrow{BM}+\overrightarrow{CM}$
D.$3\overrightarrow{AM}+\overrightarrow{AC}$
答案:
3.C 由三角形重心性质得$\overrightarrow{AM}+\overrightarrow{BM}+\overrightarrow{CM}=0$.
4. (多选)如图,在平行四边形$ABCD$中,下列计算正确的是 (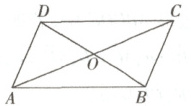
A.$\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{DO}=\overrightarrow{OA}$
B.$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$
C.$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{AD}$
D.$\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}=\boldsymbol{0}$
BCD
)
A.$\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{DO}=\overrightarrow{OA}$
B.$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$
C.$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{AD}$
D.$\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}=\boldsymbol{0}$
答案:
4.BCD 根据向量加法运算及其几何意义,相反向量的概念,$\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{DO}=\overrightarrow{DC}+\overrightarrow{CD}+\overrightarrow{DO}=\overrightarrow{DO}$,故A错误;$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$,故B正确;$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}$,故C正确;$\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{BC}+\overrightarrow{DA}=\overrightarrow{BC}+\overrightarrow{CB}=0$,故D正确.故选BCD.
5. 某人在静水中游泳,速度为$4\sqrt{3} km/h$.如果他向垂直于河对岸的方向游向河对岸,水的流速为$4 km/h$,他实际
沿与水流方向成60°的(答案不唯一)
方向前进,速度为$8 km/h$
.
答案:
5.沿与水流方向成60°的(答案不唯一)
$8 km/h$ $\because OB=4\sqrt{3},OA=4$,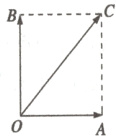
$\therefore OC=8,\therefore\angle COA=60°$.
5.沿与水流方向成60°的(答案不唯一)
$8 km/h$ $\because OB=4\sqrt{3},OA=4$,

$\therefore OC=8,\therefore\angle COA=60°$.
6. 在菱形$ABCD$中,$\angle ABC = 120^{\circ}$,向量$|\overrightarrow{AB}| = 2$,则$\left|\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{CD})\right| =$
$\sqrt{3}$
.
答案:
6.$\sqrt{3}$ 因为在菱形$ABCD$中,$\angle ABC=120°$,所以$\angle BAD=60°$,
又$AB=AD=2$,所以$\triangle ABD$为等边三角形,因此$BD=2$,连接$AC$与$BD$且交于$O$点,则$\triangle ABO$为$Rt\triangle$,且$AB=2,BO=1,AO\bot BO$,所以 $AO=\sqrt{AB^{2}-BO^{2}}=\sqrt{3}$,所以$|\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{CD})|=|\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BD}|=|\overrightarrow{AB}+\overrightarrow{BO}|=|\overrightarrow{AO}|=\sqrt{3}$.
又$AB=AD=2$,所以$\triangle ABD$为等边三角形,因此$BD=2$,连接$AC$与$BD$且交于$O$点,则$\triangle ABO$为$Rt\triangle$,且$AB=2,BO=1,AO\bot BO$,所以 $AO=\sqrt{AB^{2}-BO^{2}}=\sqrt{3}$,所以$|\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{CD})|=|\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BD}|=|\overrightarrow{AB}+\overrightarrow{BO}|=|\overrightarrow{AO}|=\sqrt{3}$.
7. 如图所示,$P,Q$是$\triangle ABC$的边$BC$上两点,且$BP = QC$. 求证:$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AP}+\overrightarrow{AQ}$.

答案:
7.$\because\overrightarrow{AB}=\overrightarrow{AP}+\overrightarrow{PB},\overrightarrow{AC}=\overrightarrow{AQ}+\overrightarrow{QC}$,
$\therefore\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AP}+\overrightarrow{PB}+\overrightarrow{AQ}+\overrightarrow{QC}$.
$\because\overrightarrow{PB}$与$\overrightarrow{QC}$大小相等,方向相反,
$\therefore\overrightarrow{PB}+\overrightarrow{QC}=0$.
故$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AP}+\overrightarrow{AQ}+0=\overrightarrow{AP}+\overrightarrow{AQ}$.
$\therefore\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AP}+\overrightarrow{PB}+\overrightarrow{AQ}+\overrightarrow{QC}$.
$\because\overrightarrow{PB}$与$\overrightarrow{QC}$大小相等,方向相反,
$\therefore\overrightarrow{PB}+\overrightarrow{QC}=0$.
故$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AP}+\overrightarrow{AQ}+0=\overrightarrow{AP}+\overrightarrow{AQ}$.
8. 如图所示,已知矩形$ABCD$中,$|\overrightarrow{AD}| = 4\sqrt{3}$,设$\overrightarrow{AB} = \boldsymbol{a},\overrightarrow{BC} = \boldsymbol{b},\overrightarrow{BD} = \boldsymbol{c}$,试求$|\boldsymbol{a} + \boldsymbol{b} + \boldsymbol{c}|$的大小.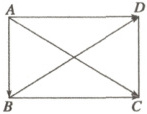

答案:
8.如图所示,过$D$作$AC$的平行线,交$BC$的延长线于点$E$.
$\because DE// AC,AD// BE$,
$\therefore$四边形$ADEC$为平行四边形,
$\therefore DE=AC,\overrightarrow{CE}=\overrightarrow{AD}$,
于是$a+b+c=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{BD}=\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{DE}+\overrightarrow{BD}=\overrightarrow{BE}=\overrightarrow{AD}+\overrightarrow{AD}$,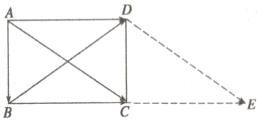
$\therefore|a+b+c|=|\overrightarrow{AD}+\overrightarrow{AD}|=8\sqrt{3}$.
8.如图所示,过$D$作$AC$的平行线,交$BC$的延长线于点$E$.
$\because DE// AC,AD// BE$,
$\therefore$四边形$ADEC$为平行四边形,
$\therefore DE=AC,\overrightarrow{CE}=\overrightarrow{AD}$,
于是$a+b+c=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{BD}=\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{DE}+\overrightarrow{BD}=\overrightarrow{BE}=\overrightarrow{AD}+\overrightarrow{AD}$,

$\therefore|a+b+c|=|\overrightarrow{AD}+\overrightarrow{AD}|=8\sqrt{3}$.
查看更多完整答案,请扫码查看


