《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

1.下列说法正确的个数是
(A)
①温度、速度、位移、功这些物理量是向量;
②零向量没有方向;
③向量的模一定是正数;
④单位向量是唯一的.

A.0
B.1
C.2
D.3

答案： 1.A温度与功没有方向，不是向量，故①错误；零向量的方向是任意的，故②错误；零向量的模可能为0，不一定是正数，故③错误；非零向量的单位向量的方向有两个，故④错误，故选A.

2.某人向正东方向行进 100 米后,再向正南方向行进$100 \sqrt{3}$米,则此人位移的方向是
(C)

A.南偏东$60°$
B.南偏东$45°$
C.南偏东$30°$
D.南偏东$15°$

答案：
2.C如图所示，此人从点A出发，经由点B，到达点C，
则$\tan\angle BAC=\frac{100\sqrt{3}}{100}=\sqrt{3}$；

$\therefore\angle BAC=60^{\circ}$，即位移的方向是东偏南$60^{\circ}$，即南偏东$30^{\circ}$，应选C.

3.设$O$是正方形$ABCD$的中心,则向量$\overrightarrow{AO},\overrightarrow{BO},\overrightarrow{OC},\overrightarrow{OD}$是
(D)

A.相等的向量
B.平行的向量
C.有相同起点的向量
D.模相等的向量

答案： 3.D这四个向量的模相等.

4.下列说法错误的是
(C)

A.$|\overrightarrow{CD}| = |\overrightarrow{DC}|$
B.$\boldsymbol{e}_1,\boldsymbol{e}_2$是单位向量,则$|\boldsymbol{e}_1| = |\boldsymbol{e}_2|$
C.若$|\overrightarrow{AB}| ＞ |\overrightarrow{CD}|$,则$\overrightarrow{AB} ＞ \overrightarrow{CD}$
D.任一非零向量都可以平行移动

答案： 4.C因为$\overrightarrow{CD}=-\overrightarrow{DC}$，所以$|\overrightarrow{CD}|=|\overrightarrow{DC}|$，故A项正确；由单位向量的定义知，$|e_1|=|e_2|=1$，故B项正确；两个向量不能比较大小，故C项错误；因为非零向量是自由向量，可以自由平行移动，故D项正确.故选C.

5.如图,在平行四边形$ABCD$中,点$E,F$分别是$AB,CD$的中点,图中与$\overrightarrow{AE}$平行的向量有
(C)


A.1 个
B.2 个
C.3 个
D.4 个

答案： 5.C根据向量的基本概念可知与$\overrightarrow{AE}$平行的向量有$\overrightarrow{BE},\overrightarrow{FD},\overrightarrow{FC}$，共3个.

6.下列说法正确的是
(C)

A.平行向量就是向量所在直线平行的向量
B.长度相等的向量叫相等向量
C.零向量的长度为 0
D.共线向量是在一条直线上的向量

答案： 6.C平行向量所在直线可以平行也可以重合，故A错；长度相等，方向不同的向量不是相等向量，故B错；共线向量即平行向量，不一定在同一条直线上，故D错.故选C.

7.零向量与单位向量的关系是共线(填"共线""相等""无关").

答案： 7.共线

8.如图,$B,C$是线段$AD$的三等分点,分别以图中各点为起点和终点,最多可以写出6个互不相等的非零向量.

答案： 8.6模为1个单位的向量有2个，如$\overrightarrow{AB},\overrightarrow{DC}$；模为2个单位的向量有2个，如$\overrightarrow{AC},\overrightarrow{DB}$；模为3个单位的向量有2个，如$\overrightarrow{AD},\overrightarrow{DA}$，故共有6个.

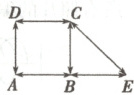
9.如图,已知四边形$ABCD$为正方形,$\triangle CBE$为等腰直角三角形,回答下列问题:
(1)图中与$\overrightarrow{AB}$共线的向量有$\overrightarrow{BA},\overrightarrow{BE},\overrightarrow{EB},\overrightarrow{AE},\overrightarrow{EA},\overrightarrow{CD},\overrightarrow{DC}$;
(2)图中与$\overrightarrow{AB}$相等的向量有$\overrightarrow{DC},\overrightarrow{BE}$;
(3)图中与$\overrightarrow{AB}$模相等的向量有$\overrightarrow{BA},\overrightarrow{BE},\overrightarrow{EB},\overrightarrow{DC},\overrightarrow{CD},\overrightarrow{AD},\overrightarrow{DA},\overrightarrow{BC},\overrightarrow{CB}$.

答案： 9.
(1)$\overrightarrow{BA},\overrightarrow{BE},\overrightarrow{EB},\overrightarrow{AE},\overrightarrow{EA},\overrightarrow{CD},\overrightarrow{DC}$
(2)$\overrightarrow{DC},\overrightarrow{BE}$
(3)$\overrightarrow{BA},\overrightarrow{BE},\overrightarrow{EB},\overrightarrow{DC},\overrightarrow{CD},\overrightarrow{AD},\overrightarrow{DA},\overrightarrow{BC},\overrightarrow{CB}$

10.如图所示,$4 × 3$的矩形(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问:

(1)与$\overrightarrow{AB}$相等的向量共有几个;
(2)与$\overrightarrow{AB}$平行且模为$\sqrt{2}$的向量共有几个?
(3)与$\overrightarrow{AB}$方向相同且模为$3 \sqrt{2}$的向量共有几个?

答案： 10.
(1)与向量$\overrightarrow{AB}$相等的向量共有5个(不包括$\overrightarrow{AB}$本身).
(2)与向量$\overrightarrow{AB}$平行且模为$\sqrt{2}$的向量共有24个.
(3)与向量$\overrightarrow{AB}$方向相同且模为$3\sqrt{2}$的向量共有2个.