《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

1. 函数$f(x)= -2\tan(2x+\frac{\pi}{6})$的定义域是 (D)

A.$\{x|x\neq \frac{\pi}{6}\}$
B.$\{x|x\neq -\frac{\pi}{12}\}$
C.$\{x|x\neq \pi+\frac{\pi}{6},k\in \mathbf{Z}\}$
D.$\{x|x\neq \frac{k\pi}{2}+\frac{\pi}{6},k\in \mathbf{Z}\}$

答案： 1.D 由正切函数的定义域，令2x + $\frac{\pi}{6}$ ≠ kπ + $\frac{\pi}{2}$，k ∈ Z，即x ≠ $\frac{k\pi}{2}$ + $\frac{\pi}{6}$(k ∈ Z)，所以函数f(x) = -2tan(2x + $\frac{\pi}{6}$)的定义域为{x|x ≠ $\frac{k\pi}{2}$ + $\frac{\pi}{6}$，k ∈ Z}，故选D。

2. $\tan x\geqslant1$的解集为 (D)

A.$\{x|x\geqslant k\pi+\frac{\pi}{4},k\in \mathbf{Z}\}$
B.$\{x|x\geqslant2k\pi+\frac{\pi}{4},k\in \mathbf{Z}\}$
C.$\{x|x\geqslant\frac{\pi}{4}\}$
D.$\{x|k\pi+\frac{\pi}{4}\leqslant x＜k\pi+\frac{\pi}{2},k\in \mathbf{Z}\}$

答案：
2.D 作函数y = tanx，x ∈ (-$\frac{\pi}{2}$，$\frac{\pi}{2}$)的图象，作函数y = 1的图象，观察图象可得当$\frac{\pi}{4}$ ≤ x ＜ $\frac{\pi}{2}$时，tanx ≥ 1，即x ∈ (-$\frac{\pi}{2}$，$\frac{\pi}{2}$)时，不等式tanx ≥ 1的解集为{x|$\frac{\pi}{4}$ ≤ x ＜ $\frac{\pi}{2}$}。正切函数y = tanx为周期函数，周期为π，所以不等式tanx ≥ 1的解集为{x|kπ + $\frac{\pi}{4}$ ≤ x ＜ kπ + $\frac{\pi}{2}$，k ∈ Z}，故选D。
　　　　

3. 函数$f(x)=\tan(\omega x-\frac{\pi}{4})$与函数$g(x)=\sin(\frac{\pi}{4}-2x)$的最小正周期相同,则$\omega=$ (A)

A.$\pm1$
B.$1$
C.$\pm2$
D.$2$

答案： 3.A $\frac{\pi}{|\omega|}=\frac{2\pi}{|2|}$，$\omega$ = ±1。

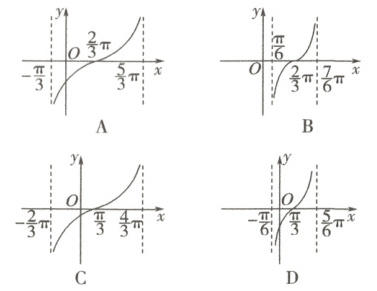
4. 函数$y=\tan(\frac{1}{2}x-\frac{\pi}{3})$在一个周期内的图象是 (A)

答案： 4.A 由f(x) = tan($\frac{1}{2}$x - $\frac{\pi}{3}$)，
知f(x + 2π) = tan[$\frac{1}{2}$(x + 2π) - $\frac{\pi}{3}$]
= tan($\frac{1}{2}$x - $\frac{\pi}{3}$) = f(x)。
∴f(x)的周期为2π，排除B，D。
令tan($\frac{1}{2}$x - $\frac{\pi}{3}$) = 0，得$\frac{x}{2}$ - $\frac{\pi}{3}$ = kπ(k ∈ Z)。
∴x = 2kπ + $\frac{2\pi}{3}$(k ∈ Z)，若k = 0，则x = $\frac{2\pi}{3}$，
即图象过点($\frac{2\pi}{3}$，0)，故选A。

5. 函数$y=\tan(\frac{\pi}{6}-x)$的定义域为$(\frac{2\pi}{3},\frac{3\pi}{2})$,则函数的值域为 (C)

A.$(\sqrt{3},+\infty)$
B.$(-\frac{\sqrt{3}}{3},+\infty)$
C.$(-\sqrt{3},+\infty)$
D.$(\frac{\sqrt{3}}{3},+\infty)$

答案： 5.C 由$\frac{2\pi}{3}$ ＜ x ＜ $\frac{3\pi}{2}$，即 -$\frac{3\pi}{2}$ ＜ -x ＜ -$\frac{2\pi}{3}$，得$\frac{\pi}{6}$ - $\frac{3\pi}{2}$ ＜ $\frac{\pi}{6}$ - x ＜ $\frac{\pi}{6}$ - $\frac{2\pi}{3}$，即 -$\frac{4\pi}{3}$ ＜ $\frac{\pi}{6}$ - x ＜ -$\frac{\pi}{2}$，从而tan($\frac{\pi}{6}$ - x) ＞ tan(-$\frac{4\pi}{3}$) = -$\sqrt{3}$。故函数的值域为(-$\sqrt{3}$，+∞)。

6. 在区间$[-2\pi,2\pi]$内,函数$y = \tan x$与函数$y = \sin x$的图象交点的个数为 (B)

A.$3$
B.$5$
C.$7$
D.$9$

答案： 6.B 在同一直角坐标系中画出函数y = tanx与函数y = sinx在区间[-2π，2π]内的图象(图象略)，由图象可知其交点个数为5，故选B。

7. 函数$y = 3\tan(2x+\frac{\pi}{3})$的对称中心的坐标为($\frac{k\pi}{4}$ - $\frac{\pi}{6}$，0)(k ∈ Z).

答案： 7.($\frac{k\pi}{4}$ - $\frac{\pi}{6}$，0)(k ∈ Z) 令2x + $\frac{\pi}{3}$ = $\frac{k\pi}{2}$(k ∈ Z)，
得x = $\frac{k\pi}{4}$ - $\frac{\pi}{6}$(k ∈ Z)，
∴对称中心的坐标为($\frac{k\pi}{4}$ - $\frac{\pi}{6}$，0)(k ∈ Z)。

8. 函数$y=\tan(-\frac{1}{2}x+\frac{\pi}{4})$的单调区间是(2kπ - $\frac{\pi}{2}$，2kπ + $\frac{3\pi}{2}$)(k ∈ Z).

答案： 8.(2kπ - $\frac{\pi}{2}$，2kπ + $\frac{3\pi}{2}$)(k ∈ Z) y = tan(-$\frac{1}{2}$x + $\frac{\pi}{4}$)
= -tan($\frac{1}{2}$x - $\frac{\pi}{4}$)，
由kπ - $\frac{\pi}{2}$ ＜ $\frac{1}{2}$x - $\frac{\pi}{4}$ ＜ kπ + $\frac{\pi}{2}$(k ∈ Z)，
得2kπ - $\frac{\pi}{2}$ ＜ x ＜ 2kπ + $\frac{3\pi}{2}$，k ∈ Z，
∴函数y = tan(-$\frac{1}{2}$x + $\frac{\pi}{4}$)的单调递减区间是(2kπ - $\frac{\pi}{2}$，2kπ + $\frac{3\pi}{2}$)，k ∈ Z。

9. 函数$f(x)=\tan ax(a＞0)$的图象的相邻两支截直线$y=\frac{\pi}{3}$所得线段长为$2$,则$a$的值为$\frac{\pi}{2}$.

答案： 9.$\frac{\pi}{2}$ 由题意可得T = 2，所以$\frac{\pi}{a}$ = 2，a = $\frac{\pi}{2}$。

10. 已知函数$f(x)=2\tan(kx-\frac{\pi}{3})$的最小正周期$T$满足$1＜T＜\frac{3}{2}$,求正整数$k$的值,并写出$f(x)$的奇偶性、单调区间.

答案： 10.因为1 ＜ T ＜ $\frac{3}{2}$，
所以1 ＜ $\frac{\pi}{k}$ ＜ $\frac{3}{2}$，即$\frac{2\pi}{3}$ ＜ k ＜ π，
因为k ∈ N*，所以k = 3，则f(x) = 2tan(3x - $\frac{\pi}{3}$)，
由3x - $\frac{\pi}{3}$ ≠ $\frac{\pi}{2}$ + kπ，k ∈ Z得x ≠ $\frac{5\pi}{18}$ + $\frac{k\pi}{3}$，k ∈ Z，所以定义域不关于原点对称，
所以f(x) = 2tan(3x - $\frac{\pi}{3}$)是非奇非偶函数。
由 -$\frac{\pi}{2}$ + kπ ＜ 3x - $\frac{\pi}{3}$ ＜ $\frac{\pi}{2}$ + kπ，k ∈ Z，
得 -$\frac{\pi}{18}$ + $\frac{k\pi}{3}$ ＜ x ＜ $\frac{5\pi}{18}$ + $\frac{k\pi}{3}$，k ∈ Z，
所以f(x) = 2tan(3x - $\frac{\pi}{3}$)的单调增区间为(-$\frac{\pi}{18}$ + $\frac{k\pi}{3}$，$\frac{5\pi}{18}$ + $\frac{k\pi}{3}$)，k ∈ Z。