《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

1.等腰梯形$ABCD$中,对角线$AC$与$BD$相交于点$P$,点$E$,点$F$分别在两腰$AD,BC$上,$EF$过点$P$且$EF // AB$,则下列等式正确的是
(D)

A.$\overrightarrow{AD} = \overrightarrow{BC}$
B.$\overrightarrow{AC} = \overrightarrow{BD}$
C.$\overrightarrow{PE} = \overrightarrow{PF}$
D.$\overrightarrow{EP} = \overrightarrow{PF}$

答案： 1.D由相等向量的定义，显然$\overrightarrow{EP}=\overrightarrow{PF}$.

2.锐角三角形$ABC$中,关于向量夹角的说法正确的是
(B)

A.$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角是锐角
B.$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角是锐角
C.$\overrightarrow{AC}$与$\overrightarrow{BC}$的夹角是钝角
D.$\overrightarrow{AC}$与$\overrightarrow{CB}$的夹角是锐角

答案： 2.B由两向量夹角的定义知，$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角的大小是$180^{\circ}-\angle B$，为钝角，$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角是$\angle A$，为锐角，$\overrightarrow{AC}$与$\overrightarrow{BC}$的夹角与$\angle C$的大小相等，为锐角，$\overrightarrow{AC}$与$\overrightarrow{CB}$的夹角的大小是$180^{\circ}-\angle C$，为钝角.

3.(多选)已知$\boldsymbol{a},\boldsymbol{b}$为两个单位向量,下列四个命题中正确的是
(BD)

A.$\boldsymbol{a}$与$\boldsymbol{b}$相等
B.如果$\boldsymbol{a}$与$\boldsymbol{b}$同向,那么$\boldsymbol{a}$与$\boldsymbol{b}$相等
C.$\boldsymbol{a} + \boldsymbol{b} = 2$
D.$|\boldsymbol{a}| = |\boldsymbol{b}|$

答案： 3.BD向量$a,b$为两个单位向量，但方向不一定相同，所以A错误；因为向量$a,b$为两个单位向量，即$|a|=|b|$，若$a$与$b$同向，则向量$a$与$b$相等，所以B正确；向量$a,b$为两个单位向量，根据向量的加法，可得$a+b$为向量，所以C错误；向量$a,b$为两个单位向量，即$|a|=|b|$，所以D正确.故选BD.

4.(多选)如图,在菱形$ABCD$中,$\angle DAB = 120°$,则以下说法正确的是
(ABC)


A.与$\overrightarrow{AB}$相等的向量只有一个(不含$\overrightarrow{AB}$)
B.与$\overrightarrow{AB}$的模相等的向量有 9 个(不含$\overrightarrow{AB}$)
C.$\overrightarrow{BD}$的模恰好为$\overrightarrow{DA}$的模的$\sqrt{3}$倍
D.$\overrightarrow{CB}$与$\overrightarrow{DA}$不共线

答案：
4.ABC与$\overrightarrow{AB}$相等的向量只有$\overrightarrow{DC}$，A正确；由已知条件可得$|\overrightarrow{AB}|=|\overrightarrow{BA}|=|\overrightarrow{BC}|=|\overrightarrow{CB}|=|\overrightarrow{AC}|=|\overrightarrow{CA}|=|\overrightarrow{DC}|=|\overrightarrow{CD}|=|\overrightarrow{DA}|=|\overrightarrow{AD}|$，B正确；如图，过点B作DA的垂线交DA的延长线于E，因为$\angle DAB=120^{\circ}$，四边形ABCD为菱形，所以$\angle BDE=\angle ABE=30^{\circ}$，在$\mathrm{Rt}\triangle BED$中，$|\overrightarrow{DB}|=\frac{|\overrightarrow{DE}|}{\cos30^{\circ}}$，在$\mathrm{Rt}\triangle AEB$中，$|\overrightarrow{AE}|=\frac{1}{2}|\overrightarrow{AB}|=\frac{1}{2}|\overrightarrow{AD}|$，所以$|\overrightarrow{DB}|=\frac{\frac{3}{2}|\overrightarrow{DA}|}{\frac{\sqrt{3}}{2}}=\sqrt{3}|\overrightarrow{DA}|$，C正确；$\overrightarrow{CB}$与$\overrightarrow{DA}$方向相同，大小相等，故$\overrightarrow{CB}=\overrightarrow{DA}$，$\overrightarrow{CB}$与$\overrightarrow{DA}$共线，D错误.故选ABC.

5.把同一平面内所有模不小于 1,不大于 2 的向量的起点,移到同一点$O$,则这些向量的终点构成的图形的面积等于$3\pi$.

答案： 5.$3\pi$这些向量的终点构成的图形是一个圆环，其面积为$\pi·2^2-\pi·1^2=3\pi$.

6.有下列说法:
①若$\boldsymbol{a} \neq \boldsymbol{b}$,则$\boldsymbol{a}$一定不与$\boldsymbol{b}$共线;
②若$\overrightarrow{AB} = \overrightarrow{DC}$,则$A,B,C,D$四点是平行四边形的四个顶点;
③在$□ ABCD$中,一定有$\overrightarrow{AD} = \overrightarrow{BC}$;
④若$\boldsymbol{a} = \boldsymbol{b},\boldsymbol{b} = \boldsymbol{c}$,则$\boldsymbol{a} = \boldsymbol{c}$;
⑤方向为南偏西$60°$的向量与北偏东$60°$的向量是共线向量.
其中,正确的说法是③④⑤.

答案： 6.③④⑤①两个向量不相等，可能是长度不相等，方向相同或相反，所以a与b有共线的可能，故①不正确；②A，B，C，D四点可能在同一条直线上，故②不正确；③在平行四边形ABCD中，$|\overrightarrow{AD}|=|\overrightarrow{BC}|$，$\overrightarrow{AD}$与$\overrightarrow{BC}$平行且方向相同，所以$\overrightarrow{AD}=\overrightarrow{BC}$，故③正确；④$a=b$，则$|a|=|b|$，且a与b方向相同；$b=c$，则$|b|=|c|$，且b与c方向相同，所以a与c方向相同且模相等，故$a=c$，故④正确；⑤南偏西$60^{\circ}$和北偏东$60^{\circ}$是两个共线，方向相反，所以两个向量是共线向量，故⑤正确.

7.如图所示,某人从点$A$出发,向西走了 200 m 后到达$B$点,然后改变方向,沿北偏西一定角度的某方向行走了$100 \sqrt{13}$m 到达$C$点,最后又改变方向,向东走了 200 m 到达$D$点,发现$D$点在$B$点的正北方.

(1)作出向量$\overrightarrow{AB},\overrightarrow{BC},\overrightarrow{CD}$(图中 1 个单位长度表示 100 m);
(2)求向量$\overrightarrow{DA}$的模.

答案：
7.
(1)如图，$\overrightarrow{AB},\overrightarrow{BC},\overrightarrow{CD}$即为所求.
(2)如图，作向量$\overrightarrow{DA}$，由题意可知，四边形ABCD是平行四边形，
$\therefore|\overrightarrow{DA}|=|\overrightarrow{BC}|=100\sqrt{13}\mathrm{m}$.

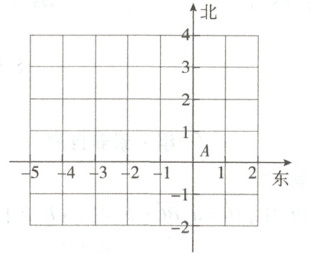
8.如图所示的方格纸由若干个边长为 1 的小正方形组成,方格纸中有两个定点$A,B$,点$C$为小正方形的顶点,且$|\overrightarrow{AC}| = \sqrt{5}$.

(1)画出所有的向量$\overrightarrow{AC}$;
(2)求$|\overrightarrow{BC}|$的最大值与最小值.

答案：
8.
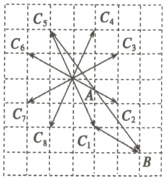
(1)画出所有的向量$\overrightarrow{AC}$如图所示.

(2)由
(1)所画的图知，
①当点C位于点$C_1$或$C_2$时，$|\overrightarrow{BC}|$取得最小值$\sqrt{1^2+2^2}=\sqrt{5}$；
②当点C位于点$C_5$或$C_6$时，$|\overrightarrow{BC}|$取得最大值$\sqrt{4^2+5^2}=\sqrt{41}$.
$\therefore|\overrightarrow{BC}|$的最大值为$\sqrt{41}$，最小值为$\sqrt{5}$.