《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

4.(多选)从物理学知识可知，图中弹簧振子中的小球相对平衡位置的位移$y$与时间$t$(单位：s)的关系符合函数$y = A\sin(\omega t+\varphi)(|\omega|＜100)$.从某一时刻开始，用相机的连拍功能给弹簧振子连拍了20张照片.已知连拍的间隔为$0.01 s$，将照片按拍照的时间先后顺序编号，发现仅有第5张、第13张、第17张照片与第1张照片是完全一样的，则小球正好处于平衡位置的所有照片的编号有
(BCD)


A.$4$
B.$6$
C.$12$
D.$18$

答案： 4.BCD 因为仅有第$5$张，第$13$张，第$17$张照片与第$1$张照片完全一样，则弹簧振子运动时的最小正周期为$T = 12 × 0.01 = 0.12 = \frac{3}{25}s$，则$\omega = \frac{2\pi}{T} = \frac{50\pi}{3}$，所以$y = A\sin(\frac{50\pi}{3}t + \varphi)$，由题意可知，$A\sin(\frac{50\pi}{3} × \frac{1}{100} + \varphi) = A\sin(\frac{50\pi}{3} × \frac{5}{100} + \varphi)$，所以$\sin(\frac{\pi}{6} + \varphi) = \sin(\frac{5\pi}{6} + \varphi)$，则$\frac{1}{2}\cos\varphi + \frac{\sqrt{3}}{2}\sin\varphi = \frac{1}{2}\cos\varphi - \frac{\sqrt{3}}{2}\sin\varphi$，所以$\sin\varphi = 0$，则$\varphi = m\pi$，$(m \in \mathbf{Z})$，则$y = A\sin(\frac{50\pi}{3}t + m\pi)$，令$y = 0$，可得$\frac{50\pi}{3}t + m\pi = n\pi(m,n \in \mathbf{Z})$，所以$t = \frac{3}{50}(n - m)$，令$k = n - m \in \mathbf{Z}$，则$t = \frac{3}{50}k(k \in \mathbf{Z})$，由$0 ＜ \frac{3k}{50} \leqslant \frac{1}{5}$，可得$0 ＜ k \leqslant \frac{10}{3}$，因为$k \in \mathbf{Z}$，则$k \in \{1,2,3\}$，当$k = 1$时，$t = \frac{3}{50} = 0.06\ s$，对应第$6$张照片，当$k = 2$时，$t = \frac{6}{50} = 0.12\ s$，对应第$12$张照片，当$k = 3$时，$t = \frac{9}{50} = 0.18\ s$，对应第$18$张照片.故选BCD.

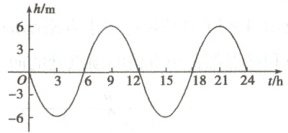
5.如图是相对于平均海平面的某海湾的水面高度$h$(米)在某天从0~24时的变化情况,则水面高度$h$关于时间$t$的函数关系式为$h = -6\sin\frac{\pi}{6}t$.

答案： 5.$h = -6\sin\frac{\pi}{6}t$

6.一个物体相对于某一固定位置的位移$y( cm)$和时间$t( s)$之间的一组对应值如下表所示：

则可近似地描述该物体的位移$y$和时间$t$之间关系的一个三角函数为$y = 4\sin(\frac{5\pi}{2}t - \frac{\pi}{2})$，$t \in [0, + \infty)$（答案不唯一）.

答案： 6.$y = 4\sin(\frac{5\pi}{2}t - \frac{\pi}{2})$，$t \in [0, + \infty)$（答案不唯一）设$y = A\sin(\omega t + \varphi) + b$，则$A = \frac{y_{\max} - y_{\min}}{2} = \frac{4.0 + 4.0}{2} = 4.0$，$b = \frac{y_{\max} + y_{\min}}{2} = 0$，$\omega = \frac{2\pi}{T} = \frac{2\pi}{0.8} = \frac{5\pi}{2}$，所以$y = 4\sin(\frac{5\pi}{2}t + \varphi)$，将$(0.4,4.0)$代入上式，得$\varphi = - \frac{\pi}{2} + 2k\pi$，$k \in \mathbf{Z}$，取$\varphi = - \frac{\pi}{2}$，从而可知$y = 4\sin(\frac{5\pi}{2}t - \frac{\pi}{2})$，$t \in [0, + \infty)$.

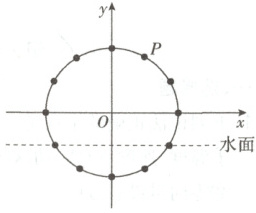
7.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中使用,明朝科学家徐光启所著《农政全书》中描绘了筒车的工作原理.如图，一个半径为$3 m$的筒车，按逆时针方向转一周的时长为$2 min$，筒车的轴心$O$距离水面的高度为$1.5 m$，筒车上均匀分布了12个盛水筒，设筒车上的某个盛水筒$P$到水面的距离为$y$(单位：m)(在水面下则$y$为负数)，若以盛水筒$P$刚浮出水面时开始计算时间，则$y$与时间$t$(单位：min)之间的关系为$y = A\sin(\omega t+\varphi)+b(A＞0,\omega＞0,|\varphi|＜\frac{\pi}{2})$.
(1)求$A,\omega,\varphi,b$的值；
(2)盛水筒出水后至少经过多长时间就可以到达最高点?

答案： 7.
(1)由题易知$\begin{cases} \frac{A + b}{2} = \frac{9}{2} \\ \frac{-A + b}{2} = - \frac{3}{2} \end{cases}$，解得$A = 3$，$b = \frac{3}{2}$.由题知$T = 2 = \frac{2\pi}{\omega}$，得$\omega = \pi$，$\therefore y = 3\sin(\pi t + \varphi) + \frac{3}{2}$，$\therefore 0 = 3\sin\varphi + \frac{3}{2}$，$|\varphi| ＜ \frac{\pi}{2}$，$\therefore \varphi = - \frac{\pi}{6}$，$\therefore A = 3$，$\omega = \pi$，$b = \frac{3}{2}$，$\varphi = - \frac{\pi}{6}$.
(2)由$y = 3\sin(\pi t - \frac{\pi}{6}) + \frac{3}{2} = \frac{9}{2}$，得$\sin(\pi t - \frac{\pi}{6}) = 1$，$\therefore \pi t - \frac{\pi}{6} = \frac{\pi}{2} + 2k\pi$，$k \in \mathbf{N}$，即$t = \frac{2}{3} + 2k$，$k \in \mathbf{N}$.当$k = 0$时，盛水筒出水后第一次到达最高点，此时$t = \frac{2}{3}min$，即盛水筒出水后至少经过$\frac{2}{3}min$就可以到达最高点.