2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
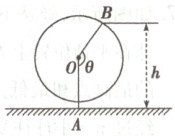
9.如图为一个缆车示意图,缆车半径为$4.8 m$,圆上最低点与地面的距离为$0.8 m,60 s$转动一圈,图中$OA$与地面垂直,以$OA$为始边,逆时针转动$\theta$角到$OB$,设$B$点与地面距离是$h$.
(1)求$h$与$\theta$间的函数解析式;
(2)设从$OA$开始转动,经过$t s$后到达$OB$,求$h$与$t$之间的函数解析式,并求缆车到达最高点时用的最少时间是多少?
(1)求$h$与$\theta$间的函数解析式;
(2)设从$OA$开始转动,经过$t s$后到达$OB$,求$h$与$t$之间的函数解析式,并求缆车到达最高点时用的最少时间是多少?

答案:
9.
(1)以圆心$O$为原点,建立如图所示的坐标系,则以$Ox$为始边,$OB$为终边的角为$\theta - \frac{\pi}{2}$,
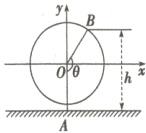
故$B$点坐标为$(4.8\cos(\theta - \frac{\pi}{2}),4.8\sin(\theta - \frac{\pi}{2}))$,所以$h = 5.6 + 4.8\sin(\theta - \frac{\pi}{2})$.
(2)点$A$在圆上转动的角速度是$\frac{\pi}{30}$,故$t\ s$转过的弧度数为$\frac{\pi}{30}t$,所以$h = 5.6 + 4.8\sin(\frac{\pi}{30}t - \frac{\pi}{2})$,$t \in [0, + \infty)$.到达最高点时,$h = 10.4$m.由$\sin(\frac{\pi}{30}t - \frac{\pi}{2}) = 1$,得$\frac{\pi}{30}t - \frac{\pi}{2} = \frac{\pi}{2} + 2k\pi$,$k \in \mathbf{N}$,所以$t_{\min} = 30(s)$,即缆车到达最高点时,用的时间最少为30秒.
9.
(1)以圆心$O$为原点,建立如图所示的坐标系,则以$Ox$为始边,$OB$为终边的角为$\theta - \frac{\pi}{2}$,

故$B$点坐标为$(4.8\cos(\theta - \frac{\pi}{2}),4.8\sin(\theta - \frac{\pi}{2}))$,所以$h = 5.6 + 4.8\sin(\theta - \frac{\pi}{2})$.
(2)点$A$在圆上转动的角速度是$\frac{\pi}{30}$,故$t\ s$转过的弧度数为$\frac{\pi}{30}t$,所以$h = 5.6 + 4.8\sin(\frac{\pi}{30}t - \frac{\pi}{2})$,$t \in [0, + \infty)$.到达最高点时,$h = 10.4$m.由$\sin(\frac{\pi}{30}t - \frac{\pi}{2}) = 1$,得$\frac{\pi}{30}t - \frac{\pi}{2} = \frac{\pi}{2} + 2k\pi$,$k \in \mathbf{N}$,所以$t_{\min} = 30(s)$,即缆车到达最高点时,用的时间最少为30秒.
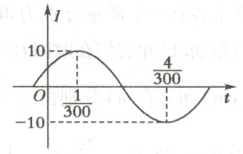
1.电流强度$I$(安培)随时间$t$(秒)变化的函数$I = A\sin(\omega t+\varphi)$的图象如图所示,则$t$为$\frac{7}{120}$(秒)时的电流强度为
(
A.$0$安培
B.$-5\sqrt{2}$安培
C.$10\sqrt{2}$安培
D.$-10\sqrt{2}$安培
(
A
)
A.$0$安培
B.$-5\sqrt{2}$安培
C.$10\sqrt{2}$安培
D.$-10\sqrt{2}$安培
答案:
1.A 由图知,$A = 10$,函数的周期$T = 2(\frac{4}{300} - \frac{1}{300}) = \frac{1}{50}$,所以$\omega = \frac{2\pi}{T} = \frac{2\pi}{\frac{1}{50}} = 100\pi$,将点$(\frac{1}{300},10)$代入$I = 10\sin(100\pi t + \varphi)$得$\varphi = \frac{\pi}{6}$,故函数解析式为$I = 10\sin(100\pi t + \frac{\pi}{6})$,再将$t = \frac{7}{120}$代入函数解析式得$I = 0$.
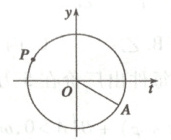
2.如图是一个半径为$R$的水车,一个水斗从点$A(3\sqrt{3}, - 3)$出发,沿圆周按逆时针方向匀速旋转,且旋转一周时用时60秒.经过$t$秒后,水斗旋转到$P$点,设$P$的坐标为$(x,y)$,其纵坐标满足$y = f(t) = R\sin(\omega t+\varphi)(t\geq0,\omega>0,|\varphi|<\frac{\pi}{2})$.则下列叙述错误的是 (
A.$R = 6,\omega=\frac{\pi}{30},\varphi=-\frac{\pi}{6}$
B.当$t\in[35,55]$时,点$P$到$x$轴的距离的最大值为$6$
C.当$t\in[10,25]$时,函数$y = f(t)$单调递减
D.当$t = 20$时,$|PA| = 6\sqrt{3}$
C
)
A.$R = 6,\omega=\frac{\pi}{30},\varphi=-\frac{\pi}{6}$
B.当$t\in[35,55]$时,点$P$到$x$轴的距离的最大值为$6$
C.当$t\in[10,25]$时,函数$y = f(t)$单调递减
D.当$t = 20$时,$|PA| = 6\sqrt{3}$
答案:
2.C 由题意,$R = \sqrt{27 + 9} = 6$,$T = 60$,$\therefore \omega = \frac{\pi}{30}$.由题意可知,当$t = 0$时,$y = -3$即$-3 = 6\sin\varphi$,$|\varphi| < \frac{\pi}{2}$,$\therefore \varphi = - \frac{\pi}{6}$.故A正确;$f(t) = 6\sin(\frac{\pi}{30}t - \frac{\pi}{6})$,当$t \in [35,55]$时,$\frac{\pi}{30}t - \frac{\pi}{6} \in [\pi,\frac{5}{3}\pi]$,$\therefore$点$P$到$x$轴的距离的最大值为$6$,故B正确;当$t \in [10,25]$时,$\frac{\pi}{30}t - \frac{\pi}{6} \in [\frac{\pi}{6},\frac{2\pi}{3}]$,函数$y = f(t)$先增后减,故C不正确;当$t = 20$时,$\frac{\pi}{30}t - \frac{\pi}{6} = \frac{\pi}{2}$,$P$的纵坐标为$6$,$|PA| = \sqrt{27 + 81} = 6\sqrt{3}$,故D正确.故选C.
3.(多选)如图所示的是一质点做简谐运动的图象,则下列结论正确的是
(
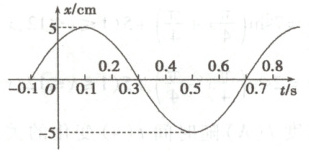
A.该质点的运动周期为$0.7 s$
B.该质点的振幅为$5$
C.该质点在$0.1 s$和$0.5 s$时运动速度为零
D.该质点的运动周期为$0.8 s$
(
BCD
)
A.该质点的运动周期为$0.7 s$
B.该质点的振幅为$5$
C.该质点在$0.1 s$和$0.5 s$时运动速度为零
D.该质点的运动周期为$0.8 s$
答案:
3.BCD 由题图可知,振动周期为$2 × (0.7 - 0.3) = 0.8\ s$,故A错误,D正确;该质点的振幅为$5$,B正确;由简谐运动的特点知,质点处于平衡位置时的速度最大,即在$0.3\ s$和$0.7\ s$时运动速度最大,在$0.1\ s$和$0.5\ s$时运动速度为零,故C正确.故选BCD.
查看更多完整答案,请扫码查看


