《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

1. 函数$y = \sin(\frac{\pi}{2}x + 3)$的相位是 (D)

A.2
B.$\frac{\pi}{2}$
C.3
D.$\frac{\pi}{2}x + 3$

答案： 1.D

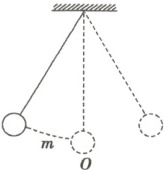
2. 如图,单摆从某点开始来回摆动,离开平衡位置$O$的距离$m$ $\mathrm{cm}$和时间$t$ $\mathrm{s}$的函数关系式为$m = \sin(t + \frac{\pi}{6})$,那么单摆来回摆动一次所需的时间为 (A)


A.$2\pi$ $\mathrm{s}$
B.$\pi$ $\mathrm{s}$
C.$0.5$ $\mathrm{s}$
D.$1$ $\mathrm{s}$

答案： 2.A $T = \frac {2\pi}{\omega} = \frac{2\pi}{1} = 2\pi$

3. 已知简谐运动$f(x) = 2\sin(x + 2\varphi)(|\varphi| ＜ \frac{\pi}{4})$的图象经过点$(0,1)$,则该简谐运动初相为 (A)

A.$\frac{\pi}{12}$
B.$\frac{\pi}{6}$
C.$\frac{\pi}{3}$
D.$\frac{2}{3}\pi$

答案： 3.A 因为图象过(0,1)点，
∴$\sin2\varphi = \frac{1}{2}$，
∵$-\frac{\pi}{2} ＜ 2\varphi ＜ \frac{\pi}{2}$，
∴$2\varphi = \frac{\pi}{6}$，$\varphi = \frac{\pi}{12}$。故选A。

4. 将函数$y = \sin 2x$的图象(D),可以得到函数$y = \sin(2x - \frac{\pi}{6})$的图象 (D)

A.向左平移$\frac{\pi}{6}$个单位
B.向左平移$\frac{\pi}{12}$个单位
C.向右平移$\frac{\pi}{6}$个单位
D.向右平移$\frac{\pi}{12}$个单位

答案： 4.D 由于函数$y = \sin(2x - \frac{\pi}{6}) = \sin2(x - \frac{\pi}{12})$，则将函数$y = \sin2x$的图象向右平移$\frac{\pi}{12}$个单位，可得到函数$y = \sin(2x - \frac{\pi}{6})$的图象。故选D。

5. 将函数$f(x) = \sin 2x$的图象向右平移$1$个单位长度后得到$g(x)$的图象,则$g(x) =$ (C)

A.$\sin(2x - 1)$
B.$\sin(2x + 1)$
C.$\sin(2x - 2)$
D.$\sin(2x + 2)$

答案： 5.C $f(x) = \sin2x$的图象向右平移1个单位后得到$g(x) = f(x - 1) = \sin2(x - 1) = \sin(2x - 2)$的图象。

6. 函数$y = \sin(-2x + \frac{\pi}{6})$的单调递减区间是 (C)

A.$\left[-\frac{\pi}{6} + 2k\pi,\frac{\pi}{3} + 2k\pi\right],k \in \mathbf{Z}$
B.$\left[\frac{\pi}{6} + 2k\pi,\frac{5\pi}{6} + 2k\pi\right],k \in \mathbf{Z}$
C.$\left[-\frac{\pi}{6} + k\pi,\frac{\pi}{3} + k\pi\right],k \in \mathbf{Z}$
D.$\left[\frac{\pi}{6} + k\pi,\frac{5\pi}{6} + k\pi\right],k \in \mathbf{Z}$

答案： 6.C $y = - \sin(2x - \frac{\pi}{6})$
令$2k\pi - \frac{\pi}{2} \leq 2x - \frac{\pi}{6} \leq 2k\pi + \frac{\pi}{2}$，得$k\pi - \frac{\pi}{6} \leq x \leq k\pi + \frac{\pi}{3}$$(k \in \mathbf{Z})$
∴函数的单调递减区间是$[k\pi - \frac{\pi}{6}, k\pi + \frac{\pi}{3}](k \in \mathbf{Z})$

7. 设函数$f(x) = 2\sin(\frac{\pi}{2}x + \frac{\pi}{5})$,若对任意$x \in \mathbf{R}$,都有$f(x_1) \leq f(x) \leq f(x_2)$成立,则$|x_1 - x_2|$的最小值是2.

答案： 7.2 由题意知$f(x_1)$只能恒等于 -2，$f(x_2)$只能恒等于2，最小正周期$T = 4$。
∴$|x_1 - x_2|_{\min} = \frac{T}{2} = 2$

8. 将函数$y = \sin x$的图象上所有点的横坐标缩短到原来的$\frac{1}{6}$(纵坐标不变)得$y = \sin6x$的图象.

答案： 8.$y = \sin6x$ 依题意将$y = \sin x$图象上所有点的横坐标缩短到原来的$\frac{1}{6}$后可得$y = \sin6x$的图象。

9. 函数$y = \sin 2x$的图象的对称轴方程为$x = \frac{k\pi}{2} + \frac{\pi}{4}(k \in \mathbf{Z})$,对称中心为$(\frac{k\pi}{2},0)(k \in \mathbf{Z})$,奇偶性为奇函数.

答案： 9.$x = \frac{k\pi}{2} + \frac{\pi}{4}(k \in \mathbf{Z})$ $(\frac{k\pi}{2},0)(k \in \mathbf{Z})$ 奇函数

10. 函数$y = \sin(2x + \frac{\pi}{3})$.
(1)求对称轴方程及对称中心;
(2)求周期及单调递增区间.

答案： 10.
(1) 令$y = \pm1$，即$\sin(2x + \frac{\pi}{3}) = \pm1$，则$2x + \frac{\pi}{3} = k\pi + \frac{\pi}{2}$$(k \in \mathbf{Z})$
∴$x = \frac{k\pi}{2} + \frac{\pi}{12}(k \in \mathbf{Z})$
即对称轴方程为$x = \frac{k\pi}{2} + \frac{\pi}{12}(k \in \mathbf{Z})$
令$y = 0$，即$\sin(2x + \frac{\pi}{3}) = 0$，则$2x + \frac{\pi}{3} = k\pi(k \in \mathbf{Z})$
∴$x = \frac{k\pi}{2} - \frac{\pi}{6}(k \in \mathbf{Z})$
∴函数$y = \sin(2x + \frac{\pi}{3})$的图象的对称中心为$(\frac{k\pi}{2} - \frac{\pi}{6},0)$$(k \in \mathbf{Z})$
(2)$T = \frac{2\pi}{2} = \pi$
令$\mu = 2x + \frac{\pi}{3}$，由$2k\pi - \frac{\pi}{2} \leq \mu \leq 2k\pi + \frac{\pi}{2}$
即$2k\pi - \frac{\pi}{2} \leq 2x + \frac{\pi}{3} \leq 2k\pi + \frac{\pi}{2}$
∴$k\pi - \frac{5\pi}{12} \leq x \leq k\pi + \frac{\pi}{12}$
∴单调递增区间为$[k\pi - \frac{5\pi}{12}, k\pi + \frac{\pi}{12}](k \in \mathbf{Z})$