2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.$\boldsymbol{e}_{1}$、$\boldsymbol{e}_{2}$是表示平面内所有向量的一组基底,下列四组向量中,不能作为一组基底的是(
A.$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$和$\boldsymbol{e}_{1}-\boldsymbol{e}_{2}$
B.$3\boldsymbol{e}_{1}-2\boldsymbol{e}_{2}$和$4\boldsymbol{e}_{2}-6\boldsymbol{e}_{1}$
C.$\boldsymbol{e}_{1}+2\boldsymbol{e}_{2}$和$\boldsymbol{e}_{2}+2\boldsymbol{e}_{1}$
D.$\boldsymbol{e}_{2}$和$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$
B
)A.$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$和$\boldsymbol{e}_{1}-\boldsymbol{e}_{2}$
B.$3\boldsymbol{e}_{1}-2\boldsymbol{e}_{2}$和$4\boldsymbol{e}_{2}-6\boldsymbol{e}_{1}$
C.$\boldsymbol{e}_{1}+2\boldsymbol{e}_{2}$和$\boldsymbol{e}_{2}+2\boldsymbol{e}_{1}$
D.$\boldsymbol{e}_{2}$和$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$
答案:
1.B $3\boldsymbol{e}_1 -2\boldsymbol{e}_2$与$4\boldsymbol{e}_2 -6\boldsymbol{e}_1$是共线向量,不能作为一组基底.
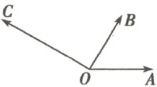
2. 如图所示,$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,$|\overrightarrow{OC}|$
$=\sqrt{3}$,$\angle AOB = 60^{\circ}$,$OB\perp OC$,设$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则(
A.$x=-2,y=-1$
B.$x=-2,y=1$
C.$x=2,y=-1$
D.$x=2,y=1$
$=\sqrt{3}$,$\angle AOB = 60^{\circ}$,$OB\perp OC$,设$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则(
B
)
A.$x=-2,y=-1$
B.$x=-2,y=1$
C.$x=2,y=-1$
D.$x=2,y=1$
答案:
2.B 方法一:过点$C$作$CD// OB$交$AO$的延长线于点$D$,连接$BC$(图略).由$|\overrightarrow{OB}| = 1,|\overrightarrow{OC}| = \sqrt{3},\angle AOB = 60^{\circ},OB\perp OC$,知$\angle COD = 30^{\circ}$.在$ Rt\triangle OCD$中,可得$OD = 2CD = 2$,则$\overrightarrow{OC} =\overrightarrow{OD} + \overrightarrow{OB} = - 2\overrightarrow{OA} + \overrightarrow{OB}$.
∴$x = - 2,y = 1$.
方法二:画图知$x<0$且$y>0$,所以选B.
∴$x = - 2,y = 1$.
方法二:画图知$x<0$且$y>0$,所以选B.
3. 在$\triangle ABC$中,$AD$为$BC$边上的中线,$E$为$AD$的中点,
则$\overrightarrow{EB}$=(
A.$\frac{3}{4}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$
B.$\frac{1}{4}\overrightarrow{AB}-\frac{3}{4}\overrightarrow{AC}$
C.$\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$
D.$\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$
则$\overrightarrow{EB}$=(
A
)A.$\frac{3}{4}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$
B.$\frac{1}{4}\overrightarrow{AB}-\frac{3}{4}\overrightarrow{AC}$
C.$\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$
D.$\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$
答案:
3.A $\overrightarrow{EB} = \overrightarrow{EA} + \overrightarrow{AB} = - \frac{1}{2}\overrightarrow{AD} + \overrightarrow{AB} = - \frac{1}{2}×\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) + \overrightarrow{AB} = \frac{3}{4}\overrightarrow{AB} - \frac{1}{4}\overrightarrow{AC}$.
4. 已知$\triangle ABC$和点$M$满足$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\boldsymbol{0}$.若存在实
数$m$使得$\overrightarrow{AB}+\overrightarrow{AC}=m\overrightarrow{AM}$成立,则$m=$
(
A.2
B.3
C.4
D.5
数$m$使得$\overrightarrow{AB}+\overrightarrow{AC}=m\overrightarrow{AM}$成立,则$m=$
(
B
)A.2
B.3
C.4
D.5
答案:
4.B 由$\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} =\boldsymbol{0}$可知,$M$为$\triangle ABC$的重心,故$\overrightarrow{AM} =\frac{2}{3}×\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) = \frac{1}{3}(\overrightarrow{AB} + \overrightarrow{AC})$,所以$\overrightarrow{AB} + \overrightarrow{AC} = 3\overrightarrow{AM}$,即$m = 3$.
5. 若$k_{1}\boldsymbol{a}+k_{2}\boldsymbol{b}=0$,则$k_{1}=k_{2}=0$,那么下列对$\boldsymbol{a}$、$\boldsymbol{b}$的判
断正确的是(
A.$\boldsymbol{a}$与$\boldsymbol{b}$一定共线
B.$\boldsymbol{a}$与$\boldsymbol{b}$一定不共线
C.$\boldsymbol{a}$与$\boldsymbol{b}$一定垂直
D.$\boldsymbol{a}$与$\boldsymbol{b}$中至少一个为$\boldsymbol{0}$
断正确的是(
B
)A.$\boldsymbol{a}$与$\boldsymbol{b}$一定共线
B.$\boldsymbol{a}$与$\boldsymbol{b}$一定不共线
C.$\boldsymbol{a}$与$\boldsymbol{b}$一定垂直
D.$\boldsymbol{a}$与$\boldsymbol{b}$中至少一个为$\boldsymbol{0}$
答案:
5.B 由平面向量基本定理知,当$\boldsymbol{a},\boldsymbol{b}$不共线时,$k_1 = k_2 = 0$.故选B.
6. 在$\triangle ABC$中,$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AC}=\boldsymbol{b}$,若$\overrightarrow{AC}=2\overrightarrow{EC}$,$\overrightarrow{BC}=2\overrightarrow{DC}$,
线段$AD$与$BE$交于点$F$,则$\overrightarrow{CF}=$
(
A.$\frac{1}{3}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$
B.$\frac{1}{3}\boldsymbol{a}-\frac{2}{3}\boldsymbol{b}$
C.$-\frac{1}{3}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$
D.$-\frac{1}{3}\boldsymbol{a}-\frac{2}{3}\boldsymbol{b}$
线段$AD$与$BE$交于点$F$,则$\overrightarrow{CF}=$
(
B
)A.$\frac{1}{3}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$
B.$\frac{1}{3}\boldsymbol{a}-\frac{2}{3}\boldsymbol{b}$
C.$-\frac{1}{3}\boldsymbol{a}+\frac{2}{3}\boldsymbol{b}$
D.$-\frac{1}{3}\boldsymbol{a}-\frac{2}{3}\boldsymbol{b}$
答案:
6.B 如图所示:
由$\overrightarrow{AC} = 2\overrightarrow{EC},\overrightarrow{BC} = 2\overrightarrow{DC}$可得$D,E$分别为$BC,AC$的中点,由中线性质可得$\overrightarrow{AF} = \frac{2}{3}\overrightarrow{AD}$,又$\overrightarrow{AD} =\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) = \frac{1}{2}(\boldsymbol{a} + \boldsymbol{b})$,所以$\overrightarrow{AF} = \frac{2}{3}×\frac{1}{2}(\boldsymbol{a} + \boldsymbol{b}) = \frac{1}{3}(\boldsymbol{a} + \boldsymbol{b})$,因此$\overrightarrow{CF} =\overrightarrow{CA} + \overrightarrow{AF} = -\boldsymbol{b} + \frac{1}{3}(\boldsymbol{a} + \boldsymbol{b}) = \frac{1}{3}\boldsymbol{a} - \frac{2}{3}\boldsymbol{b}$.故选B.

6.B 如图所示:
由$\overrightarrow{AC} = 2\overrightarrow{EC},\overrightarrow{BC} = 2\overrightarrow{DC}$可得$D,E$分别为$BC,AC$的中点,由中线性质可得$\overrightarrow{AF} = \frac{2}{3}\overrightarrow{AD}$,又$\overrightarrow{AD} =\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) = \frac{1}{2}(\boldsymbol{a} + \boldsymbol{b})$,所以$\overrightarrow{AF} = \frac{2}{3}×\frac{1}{2}(\boldsymbol{a} + \boldsymbol{b}) = \frac{1}{3}(\boldsymbol{a} + \boldsymbol{b})$,因此$\overrightarrow{CF} =\overrightarrow{CA} + \overrightarrow{AF} = -\boldsymbol{b} + \frac{1}{3}(\boldsymbol{a} + \boldsymbol{b}) = \frac{1}{3}\boldsymbol{a} - \frac{2}{3}\boldsymbol{b}$.故选B.

7. 如右图,平行四边形$ABCD$中,$\overrightarrow{AB}$
$=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,$M$是$DC$的中点,以
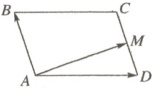
$\boldsymbol{a}$、$\boldsymbol{b}$为基底表示向量$\overrightarrow{AM}=$
_.
$=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,$M$是$DC$的中点,以

$\boldsymbol{a}$、$\boldsymbol{b}$为基底表示向量$\overrightarrow{AM}=$
$\boldsymbol{b} + \frac{1}{2}\boldsymbol{a}$
_.
答案:
7.$\boldsymbol{b} + \frac{1}{2}\boldsymbol{a}$ $\overrightarrow{AM} =\overrightarrow{AD} + \overrightarrow{DM} =\overrightarrow{AD} + \frac{1}{2}\overrightarrow{DC} =\overrightarrow{AD} + \frac{1}{2}\overrightarrow{AB} = \boldsymbol{b} + \frac{1}{2}\boldsymbol{a}$.
8. 设向量$\boldsymbol{a}$,$\boldsymbol{b}$不平行,向量$\lambda\boldsymbol{a}+\boldsymbol{b}$与$\boldsymbol{a}+3\boldsymbol{b}$平行,则实数
$\lambda =$
_.
$\lambda =$
$\frac{1}{3}$
_.
答案:
8.$\frac{1}{3}$ 依据平行向量基本定理列方程组求解.
∵$\lambda\boldsymbol{a} + \boldsymbol{b}$与$\boldsymbol{a} + 3\boldsymbol{b}$平行,
∴可设$\lambda\boldsymbol{a} + \boldsymbol{b} = t(\boldsymbol{a} + 3\boldsymbol{b})$,
即$\lambda\boldsymbol{a} + \boldsymbol{b} = t\boldsymbol{a} + 3t\boldsymbol{b}$,
$\begin{cases}\lambda = t,\\1 = 3t,\end{cases}$解得$\begin{cases}\lambda =\frac{1}{3},\\t =\frac{1}{3}.\end{cases}$
∵$\lambda\boldsymbol{a} + \boldsymbol{b}$与$\boldsymbol{a} + 3\boldsymbol{b}$平行,
∴可设$\lambda\boldsymbol{a} + \boldsymbol{b} = t(\boldsymbol{a} + 3\boldsymbol{b})$,
即$\lambda\boldsymbol{a} + \boldsymbol{b} = t\boldsymbol{a} + 3t\boldsymbol{b}$,
$\begin{cases}\lambda = t,\\1 = 3t,\end{cases}$解得$\begin{cases}\lambda =\frac{1}{3},\\t =\frac{1}{3}.\end{cases}$
9. 设$\boldsymbol{e}_{1}$,$\boldsymbol{e}_{2}$是平面内一组基向量,且$\boldsymbol{a}=\boldsymbol{e}_{1}+2\boldsymbol{e}_{2}$,$\boldsymbol{b}=$
$-\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$,则向量$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$可以表示为以$\boldsymbol{a}$,$\boldsymbol{b}$为基向量
的线性组合,即$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}=$
_.
$-\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$,则向量$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}$可以表示为以$\boldsymbol{a}$,$\boldsymbol{b}$为基向量
的线性组合,即$\boldsymbol{e}_{1}+\boldsymbol{e}_{2}=$
$\frac{2}{3}\boldsymbol{a} - \frac{1}{3}\boldsymbol{b}$
_.
答案:
9.$\frac{2}{3}\boldsymbol{a} - \frac{1}{3}\boldsymbol{b}$ 设$\boldsymbol{e}_1 + \boldsymbol{e}_2 = m\boldsymbol{a} + n\boldsymbol{b}(m,n\in\mathbf{R})$,
∵$\boldsymbol{a} =\boldsymbol{e}_1 + 2\boldsymbol{e}_2,\boldsymbol{b} = -\boldsymbol{e}_1 + \boldsymbol{e}_2$,
∴$\boldsymbol{e}_1 + \boldsymbol{e}_2 = m(\boldsymbol{e}_1 + 2\boldsymbol{e}_2) + n( -\boldsymbol{e}_1 + \boldsymbol{e}_2) = (m - n)\boldsymbol{e}_1 + (2m +n)\boldsymbol{e}_2$.
∵$\boldsymbol{e}_1$与$\boldsymbol{e}_2$不共线,
∴$\begin{cases}m - n = 1,\\2m + n = 1,\end{cases}$
$\begin{cases}m =\frac{2}{3},\\n = -\frac{1}{3}.\end{cases}$
∴$\boldsymbol{e}_1 + \boldsymbol{e}_2 =\frac{2}{3}\boldsymbol{a} - \frac{1}{3}\boldsymbol{b}$.
∵$\boldsymbol{a} =\boldsymbol{e}_1 + 2\boldsymbol{e}_2,\boldsymbol{b} = -\boldsymbol{e}_1 + \boldsymbol{e}_2$,
∴$\boldsymbol{e}_1 + \boldsymbol{e}_2 = m(\boldsymbol{e}_1 + 2\boldsymbol{e}_2) + n( -\boldsymbol{e}_1 + \boldsymbol{e}_2) = (m - n)\boldsymbol{e}_1 + (2m +n)\boldsymbol{e}_2$.
∵$\boldsymbol{e}_1$与$\boldsymbol{e}_2$不共线,
∴$\begin{cases}m - n = 1,\\2m + n = 1,\end{cases}$
$\begin{cases}m =\frac{2}{3},\\n = -\frac{1}{3}.\end{cases}$
∴$\boldsymbol{e}_1 + \boldsymbol{e}_2 =\frac{2}{3}\boldsymbol{a} - \frac{1}{3}\boldsymbol{b}$.
10. 如图所示,已知在平行四边形$ABCD$中,$E$,$F$分别是
$BC$,$DC$边上的中点.若$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,试以$\boldsymbol{a}$,$\boldsymbol{b}$为
基底表示$\overrightarrow{DE}$,$\overrightarrow{BF}$.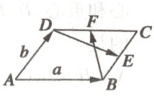
$BC$,$DC$边上的中点.若$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,试以$\boldsymbol{a}$,$\boldsymbol{b}$为
基底表示$\overrightarrow{DE}$,$\overrightarrow{BF}$.

答案:
10.
∵四边形$ABCD$是平行四边形,
$E,F$分别是$BC,DC$边上的中点,
∴$\overrightarrow{AD} =\overrightarrow{BC} = 2\overrightarrow{BE},\overrightarrow{CD} =\overrightarrow{BA} = 2\overrightarrow{CF}$,
∴$\overrightarrow{BE} =\frac{1}{2}\overrightarrow{AD} =\frac{1}{2}\boldsymbol{b}$,
$\overrightarrow{CF} =\frac{1}{2}\overrightarrow{CD} =\frac{1}{2}\overrightarrow{BA} = -\frac{1}{2}\overrightarrow{AB} = -\frac{1}{2}\boldsymbol{a}$.
∴$\overrightarrow{DE} =\overrightarrow{DA} + \overrightarrow{AB} + \overrightarrow{BE} = -\boldsymbol{AD} + \overrightarrow{AB} + \overrightarrow{BE} = -\boldsymbol{b} + \boldsymbol{a} + \frac{1}{2}\boldsymbol{b} = \boldsymbol{a} - \frac{1}{2}\boldsymbol{b}$,
$\overrightarrow{BF} =\overrightarrow{BC} + \overrightarrow{CF} =\boldsymbol{b} - \frac{1}{2}\boldsymbol{a}$.
∵四边形$ABCD$是平行四边形,
$E,F$分别是$BC,DC$边上的中点,
∴$\overrightarrow{AD} =\overrightarrow{BC} = 2\overrightarrow{BE},\overrightarrow{CD} =\overrightarrow{BA} = 2\overrightarrow{CF}$,
∴$\overrightarrow{BE} =\frac{1}{2}\overrightarrow{AD} =\frac{1}{2}\boldsymbol{b}$,
$\overrightarrow{CF} =\frac{1}{2}\overrightarrow{CD} =\frac{1}{2}\overrightarrow{BA} = -\frac{1}{2}\overrightarrow{AB} = -\frac{1}{2}\boldsymbol{a}$.
∴$\overrightarrow{DE} =\overrightarrow{DA} + \overrightarrow{AB} + \overrightarrow{BE} = -\boldsymbol{AD} + \overrightarrow{AB} + \overrightarrow{BE} = -\boldsymbol{b} + \boldsymbol{a} + \frac{1}{2}\boldsymbol{b} = \boldsymbol{a} - \frac{1}{2}\boldsymbol{b}$,
$\overrightarrow{BF} =\overrightarrow{BC} + \overrightarrow{CF} =\boldsymbol{b} - \frac{1}{2}\boldsymbol{a}$.
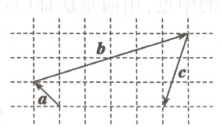
1. 向量$\boldsymbol{a}$,$\boldsymbol{b}$,$\boldsymbol{c}$在正方形网格中的位置如图所示,若$\boldsymbol{c}=$
$\lambda\boldsymbol{a}+\mu\boldsymbol{b}(\lambda,\mu\in\mathbf{R})$,则$\frac{\lambda}{\mu}=$
(
A.2
B.4
C.5
D.7
$\lambda\boldsymbol{a}+\mu\boldsymbol{b}(\lambda,\mu\in\mathbf{R})$,则$\frac{\lambda}{\mu}=$
(
B
)
A.2
B.4
C.5
D.7
答案:
1.B 以如图所示的两互相垂直的单位向量$\boldsymbol{e}_1,\boldsymbol{e}_2$为基底,

则$\boldsymbol{a} = -\boldsymbol{e}_1 + \boldsymbol{e}_2,\boldsymbol{b} = 6\boldsymbol{e}_1 + 2\boldsymbol{e}_2,\boldsymbol{c} = -\boldsymbol{e}_1 - 3\boldsymbol{e}_2$,
因为$\boldsymbol{c} =\lambda\boldsymbol{a} +\mu\boldsymbol{b}(\lambda,\mu\in\mathbf{R})$,所以$ -\boldsymbol{e}_1 - 3\boldsymbol{e}_2 =\lambda( -\boldsymbol{e}_1 + \boldsymbol{e}_2) +\mu(6\boldsymbol{e}_1 + 2\boldsymbol{e}_2) = ( -\lambda + 6\mu)\boldsymbol{e}_1 + (\lambda + 2\mu)\boldsymbol{e}_2$,
所以$\begin{cases} -\lambda + 6\mu = - 1,\\\lambda + 2\mu = - 3,\end{cases}$解得$\begin{cases}\lambda = - 2,\\\mu = -\frac{1}{2}.\end{cases}$ 所以$\frac{\lambda}{\mu} = 4$.故选B.
1.B 以如图所示的两互相垂直的单位向量$\boldsymbol{e}_1,\boldsymbol{e}_2$为基底,

则$\boldsymbol{a} = -\boldsymbol{e}_1 + \boldsymbol{e}_2,\boldsymbol{b} = 6\boldsymbol{e}_1 + 2\boldsymbol{e}_2,\boldsymbol{c} = -\boldsymbol{e}_1 - 3\boldsymbol{e}_2$,
因为$\boldsymbol{c} =\lambda\boldsymbol{a} +\mu\boldsymbol{b}(\lambda,\mu\in\mathbf{R})$,所以$ -\boldsymbol{e}_1 - 3\boldsymbol{e}_2 =\lambda( -\boldsymbol{e}_1 + \boldsymbol{e}_2) +\mu(6\boldsymbol{e}_1 + 2\boldsymbol{e}_2) = ( -\lambda + 6\mu)\boldsymbol{e}_1 + (\lambda + 2\mu)\boldsymbol{e}_2$,
所以$\begin{cases} -\lambda + 6\mu = - 1,\\\lambda + 2\mu = - 3,\end{cases}$解得$\begin{cases}\lambda = - 2,\\\mu = -\frac{1}{2}.\end{cases}$ 所以$\frac{\lambda}{\mu} = 4$.故选B.
2. (多选)如果$\boldsymbol{e}_{1}$、$\boldsymbol{e}_{2}$是平面$\alpha$内所有向量的一组基底,
那么下列命题中错误的是(
A.已知实数$\lambda_{1}$、$\lambda_{2}$,则向量$\lambda_{1}\boldsymbol{e}_{1}+\lambda_{2}\boldsymbol{e}_{2}$不一定在平面
$\alpha$内
B.对平面$\alpha$内任一向量$\boldsymbol{a}$,使$\boldsymbol{a}=\lambda_{1}\boldsymbol{e}_{1}+\lambda_{2}\boldsymbol{e}_{2}$的实数
$\lambda_{1}$,$\lambda_{2}$可以不唯一
C.若有实数$\lambda_{1}$、$\lambda_{2}$使$\lambda_{1}\boldsymbol{e}_{1}=\lambda_{2}\boldsymbol{e}_{2}$,则$\lambda_{1}=\lambda_{2}=0$
D.对平面$\alpha$内任一向量$\boldsymbol{a}$,使$\boldsymbol{a}=\lambda_{1}\boldsymbol{e}_{1}+\lambda_{2}\boldsymbol{e}_{2}$的实数
$\lambda_{1}$、$\lambda_{2}$不一定存在
那么下列命题中错误的是(
ABD
)A.已知实数$\lambda_{1}$、$\lambda_{2}$,则向量$\lambda_{1}\boldsymbol{e}_{1}+\lambda_{2}\boldsymbol{e}_{2}$不一定在平面
$\alpha$内
B.对平面$\alpha$内任一向量$\boldsymbol{a}$,使$\boldsymbol{a}=\lambda_{1}\boldsymbol{e}_{1}+\lambda_{2}\boldsymbol{e}_{2}$的实数
$\lambda_{1}$,$\lambda_{2}$可以不唯一
C.若有实数$\lambda_{1}$、$\lambda_{2}$使$\lambda_{1}\boldsymbol{e}_{1}=\lambda_{2}\boldsymbol{e}_{2}$,则$\lambda_{1}=\lambda_{2}=0$
D.对平面$\alpha$内任一向量$\boldsymbol{a}$,使$\boldsymbol{a}=\lambda_{1}\boldsymbol{e}_{1}+\lambda_{2}\boldsymbol{e}_{2}$的实数
$\lambda_{1}$、$\lambda_{2}$不一定存在
答案:
2.ABD 选项A中,由平面向量基本定理知$\lambda_1\boldsymbol{e}_1 + \lambda_2\boldsymbol{e}_2$与$\boldsymbol{e}_1,\boldsymbol{e}_2$共面,所以A项不正确;选项B中,实数$\lambda_1,\lambda_2$有且仅有一对,所以B项不正确;选项D中,实数$\lambda_1,\lambda_2$一定存在,所以D项不正确;很明显C项正确.
查看更多完整答案,请扫码查看


