《2025年成才之路高中新课程学习指导高中数学必修第二册北师大版》

1. 下列函数中最小正周期为$\pi$,且在区间$\left(0,\frac{\pi}{2}\right)$上单调递增的是
(B)

A.$y = \sin x$
B.$y=|\sin x|$
C.$y = \cos x$
D.$y=|\cos x|$

答案： 1.B 依题意，最小正周期为$T=\frac{2\pi}{1}=2\pi\neq\pi$，所以A、C选项不符合题意；$y = |\sin x|$周期为$T = \pi$，且在$(0,\frac{\pi}{2})$上单调递增，所以B选项符合题意；$y = |\cos x|$周期为$T = \pi$，且在$(0,\frac{\pi}{2})$上单调递减，所以D选项不符合题意.故选B.

2. 将下列各式按大小顺序排列,其中正确的是 (D)

A.$\cos 0＜\cos\frac{1}{2}＜\cos 1＜\cos 30^{\circ}＜\cos\pi$
B.$\cos 0＜\cos\pi＜\cos\frac{1}{2}＜\cos 30^{\circ}＜\cos 1$
C.$\cos 0＞\cos\frac{1}{2}＞ \cos 1＞\cos 30^{\circ}＞\cos\pi$
D.$\cos 0＞\cos\frac{1}{2}＞ \cos 30^{\circ}＞\cos 1＞\cos\pi$

答案： 2.D 在$[0,\frac{\pi}{2}]$上，$0＜\frac{1}{2}＜\frac{\pi}{6}＜1$，又余弦函数在$[0,\frac{\pi}{2}]$上是减少的，所以$\cos 0＞\cos\frac{1}{2}＞\cos\frac{\pi}{6}＞\cos 1＞0$。又$\cos\pi＜0$，所以$\cos 0＞\cos\frac{1}{2}＞\cos\frac{\pi}{6}＞\cos 1＞\cos\pi$.

3. (多选)已知函数$f(x)=|2\cos x|$,则 (BD)

A.函数$f(x)$的最小正周期$T = 2\pi$
B.函数$f(x)$在$\left(\frac{5\pi}{2},3\pi\right)$上单调递增
C.函数$f(x)$在$\left(-\frac{3\pi}{4},\frac{\pi}{4}\right)$上的值域为$(0,\sqrt{2})$
D.函数$f(x)$的图象关于直线$x = 2025\pi$对称

答案：
3.BD 因为$f(x)=|2\cos x| = 2|\cos x|$，
作出函数的大致图象，

函数$f(x)$的最小正周期$T = \pi$，故A错误；由图象可知函数的增区间为$[k\pi-\frac{\pi}{2},k\pi](k\in Z)$，故函数$f(x)$在$(\frac{5\pi}{2},3\pi)$上单调递增，故B正确；当$x\in(-\frac{3\pi}{4},\frac{\pi}{4})$时，$\cos x\in(-\frac{\sqrt{2}}{2},1]$，$f(x)\in[0,2]$，故C错误；因为$f(2025\pi)=2|\cos(2025\pi)| = 2$，所以函数$f(x)$的图象关于直线$x = 2025\pi$对称，故D正确.故选BD.

4. (多选)若函数$f(x)=2\cos x(0\leq x\leq2\pi)$的图象和直线$y = 2$围成一个封闭的平面图形,则下列说法正确的是
(AC)

A.当$x\in\left(\frac{\pi}{2},\frac{3\pi}{2}\right)$时,$y＜0$
B.$f(0)=1$
C.$f\left(\frac{3\pi}{2}\right)=0$
D.围成的封闭图形的面积为$2\pi$

答案：
4.AC 作出函数$y = 2\cos x$，$x\in[0,2\pi]$的图象，函数$y = 2\cos x$，$x\in[0,2\pi]$的图象与直线$y = 2$围成的平面图形为如图所示的阴影部分，由图可知，A正确；B错误；C正确；

利用图象的对称性，可知该阴影部分的面积等于矩形$OABC$的面积，又
∵$OA = 2$，$OC = 2\pi$，
∴封闭图形的面积等于$S_{矩形OABC}=2×2\pi = 4\pi$，
∴D错误.故选AC.

5. 若$\cos x=\frac{2m - 1}{3m + 2}$,且$x\in\mathbf{R}$,则$m$的取值范围是$(-\infty,-3]\cup[-\frac{1}{5},+\infty)$.

答案： 5.$(-\infty,-3]\cup[-\frac{1}{5},+\infty)$
∵$|\frac{2m - 1}{3m + 2}|=|\cos x|\leqslant1$，
∴$|2m - 1|\leqslant|3m + 2|$.
∴$(2m - 1)^2\leqslant(3m + 2)^2$.
∴$m\leqslant - 3$，或$m\geqslant-\frac{1}{5}$.
∴$m\in(-\infty,-3]\cup[-\frac{1}{5},+\infty)$.

6. 函数$y=\log_{\frac{1}{2}}\cos x$的递增区间是$[2k\pi,2k\pi+\frac{\pi}{2})(k\in Z)$.

答案： 6.$[2k\pi,2k\pi+\frac{\pi}{2})(k\in Z)$ 由题知$\cos x＞0$，$x\in(2k\pi-\frac{\pi}{2},2k\pi+\frac{\pi}{2})$，$k\in Z$.
又令$t = \cos x$，$y = \log_{\frac{1}{2}}t$，则$t = \cos x$的减区间即为$y = \log_{\frac{1}{2}}\cos x$的增区间.
∴$x\in[2k\pi,2k\pi+\frac{\pi}{2})(k\in Z)$.

7. 已知函数$f(x)=2\cos x - 1$.
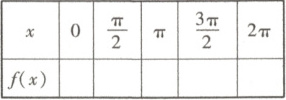
(1)完成下表格,并用五点法在下面直角坐标系中画出$f(x)$在$[0,2\pi]$上的简图;
$x$ $0$ $\frac{\pi}{2}$ $\pi$ $\frac{3\pi}{2}$ $2\pi$
$f(x)$
(2)求不等式$f(x)＞-\sqrt{3}-1$在全体实数上的解集.

答案：
7.
(1)表格如下：
$x$ $0$ $\frac{\pi}{2}$ $\pi$ $\frac{3\pi}{2}$ $2\pi$
$f(x)$ $1$ $-1$ $-3$ $-1$ $1$
用五点法在直角坐标系中画出$f(x)$在$[0,2\pi]$上的简图如下

(2)由已知$f(x)=2\cos x - 1＞-\sqrt{3}-1$，
得$\cos x＞-\frac{\sqrt{3}}{2}$，
得$-\frac{5\pi}{6}+2k\pi＜x＜\frac{5\pi}{6}+2k\pi$，$k\in Z$，
即不等式$f(x)＞-\sqrt{3}-1$在全体实数上的解集为$(-\frac{5\pi}{6}+2k\pi,\frac{5\pi}{6}+2k\pi)$，$k\in Z$.

8. 函数$f(x)=\frac{1}{2}-\frac{a}{4}+a\cos x-\cos^2x\left(0\leq x\leq\frac{\pi}{2}\right)$的最大值为$2$,求实数$a$的值.

答案： 8.令$t = \cos x$，由$0\leqslant x\leqslant\frac{\pi}{2}$，知$0\leqslant\cos x\leqslant1$，即$t\in[0,1]$.所以原函数可以转化为$y=-t^{2}+at+\frac{1}{2}-\frac{a}{4}=-(t-\frac{a}{2})^{2}+\frac{a^{2}}{4}+\frac{1}{2}-\frac{a}{4}$，$t\in[0,1]$.
①若$\frac{a}{2}\leqslant0$，即$a\leqslant0$时，当$t = 0$时，
$y_{\max}=\frac{1}{2}-\frac{a}{4}=2$，解得$a = - 6$.
②若$0＜\frac{a}{2}＜1$，即$0＜a＜2$时，当$t=\frac{a}{2}$时，
$y_{\max}=\frac{a^{2}}{4}+\frac{1}{2}-\frac{a}{4}=2$，解得$a = 3$或$a = - 2$，全舍去.
③若$\frac{a}{2}\geqslant1$，即$a\geqslant2$时，当$t = 1$时，
$y_{\max}=-1 + a+\frac{1}{2}-\frac{a}{4}=2$，解得$a=\frac{10}{3}$.
综上所述，可知$a = - 6$或$\frac{10}{3}$.