2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. (多选) 在$\triangle ABC$中,$\overrightarrow{BP} = \frac{1}{3}\overrightarrow{BA} + \frac{1}{4}\overrightarrow{BC}$,$\overrightarrow{BQ} = \frac{1}{4}\overrightarrow{BA} + \frac{1}{3}\overrightarrow{BC}$,以下结论正确的是 (
A.$\frac{S_{\triangle PBC}}{S_{\triangle ABC}} = \frac{1}{3}$
B.$\frac{S_{\triangle QBC}}{S_{\triangle ABC}} = \frac{1}{4}$
C.$\frac{S_{\triangle PAC}}{S_{\triangle QAC}} = \frac{3}{4}$
D.$\frac{S_{\triangle QAC}}{S_{\triangle ABC}} = \frac{5}{12}$
ABD
)A.$\frac{S_{\triangle PBC}}{S_{\triangle ABC}} = \frac{1}{3}$
B.$\frac{S_{\triangle QBC}}{S_{\triangle ABC}} = \frac{1}{4}$
C.$\frac{S_{\triangle PAC}}{S_{\triangle QAC}} = \frac{3}{4}$
D.$\frac{S_{\triangle QAC}}{S_{\triangle ABC}} = \frac{5}{12}$
答案:
3.ABD 由$\overrightarrow{BP}=\frac{1}{3}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}$,两边同时乘以$\frac{12}{7}$,得$\frac{12}{7}\overrightarrow{BP}=\frac{4}{7}\overrightarrow{BA}+\frac{3}{7}\overrightarrow{BC}$,令$\overrightarrow{BM}=\frac{4}{7}\overrightarrow{BA}+\frac{3}{7}\overrightarrow{BC}$,则$\frac{4}{7}\overrightarrow{BM}-\frac{4}{7}\overrightarrow{BA}=\frac{3}{7}\overrightarrow{BC}-\frac{3}{7}\overrightarrow{BM}$,即有$4\overrightarrow{AM}=3\overrightarrow{MC}$,因此$\overrightarrow{MC}=\frac{4}{7}\overrightarrow{AC}$,点$M$在$AC$上,且$\overrightarrow{BP}=\frac{7}{12}\overrightarrow{BM}$,
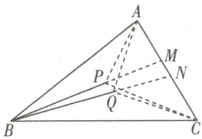
所以$S_{\triangle PBC}=\frac{7}{12}S_{\triangle MBC}$,$S_{\triangle MBC}=\frac{4}{7}S_{\triangle ABC}$,$S_{\triangle PBC}=\frac{1}{3}S_{\triangle ABC}$,则$S_{\triangle PBC}:S_{\triangle ABC}=1:3$;同理$\overrightarrow{BQ}=\frac{1}{4}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}$,两边同时乘以$\frac{12}{7}$得:$\frac{12}{7}\overrightarrow{BQ}=\frac{3}{7}\overrightarrow{BA}+\frac{4}{7}\overrightarrow{BC}$,令$\overrightarrow{BN}=\frac{3}{7}\overrightarrow{BA}+\frac{4}{7}\overrightarrow{BC}$,点$N$在$AC$上,$\overrightarrow{NC}=\frac{3}{7}\overrightarrow{AC}$,$\overrightarrow{BQ}=\frac{7}{12}\overrightarrow{BN}$,所以$S_{\triangle QBC}=\frac{7}{12}S_{\triangle NBC}$,$S_{\triangle NBC}=\frac{3}{7}S_{\triangle ABC}$,$S_{\triangle QBC}=\frac{1}{4}S_{\triangle ABC}$,则$S_{\triangle QBC}:S_{\triangle ABC}=1:4$;$\overrightarrow{BP}=\frac{7}{12}\overrightarrow{BM}$,$S_{\triangle PAC}=\frac{5}{12}S_{\triangle BAC}$,$\overrightarrow{BQ}=\frac{7}{12}\overrightarrow{BN}$,$S_{\triangle QAC}=\frac{5}{12}S_{\triangle BAC}$,所以$S_{\triangle PAC}:S_{\triangle QAC}=1:1$,$S_{\triangle QAC}:S_{\triangle ABC}=5:12$.故选ABD.
3.ABD 由$\overrightarrow{BP}=\frac{1}{3}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}$,两边同时乘以$\frac{12}{7}$,得$\frac{12}{7}\overrightarrow{BP}=\frac{4}{7}\overrightarrow{BA}+\frac{3}{7}\overrightarrow{BC}$,令$\overrightarrow{BM}=\frac{4}{7}\overrightarrow{BA}+\frac{3}{7}\overrightarrow{BC}$,则$\frac{4}{7}\overrightarrow{BM}-\frac{4}{7}\overrightarrow{BA}=\frac{3}{7}\overrightarrow{BC}-\frac{3}{7}\overrightarrow{BM}$,即有$4\overrightarrow{AM}=3\overrightarrow{MC}$,因此$\overrightarrow{MC}=\frac{4}{7}\overrightarrow{AC}$,点$M$在$AC$上,且$\overrightarrow{BP}=\frac{7}{12}\overrightarrow{BM}$,

所以$S_{\triangle PBC}=\frac{7}{12}S_{\triangle MBC}$,$S_{\triangle MBC}=\frac{4}{7}S_{\triangle ABC}$,$S_{\triangle PBC}=\frac{1}{3}S_{\triangle ABC}$,则$S_{\triangle PBC}:S_{\triangle ABC}=1:3$;同理$\overrightarrow{BQ}=\frac{1}{4}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}$,两边同时乘以$\frac{12}{7}$得:$\frac{12}{7}\overrightarrow{BQ}=\frac{3}{7}\overrightarrow{BA}+\frac{4}{7}\overrightarrow{BC}$,令$\overrightarrow{BN}=\frac{3}{7}\overrightarrow{BA}+\frac{4}{7}\overrightarrow{BC}$,点$N$在$AC$上,$\overrightarrow{NC}=\frac{3}{7}\overrightarrow{AC}$,$\overrightarrow{BQ}=\frac{7}{12}\overrightarrow{BN}$,所以$S_{\triangle QBC}=\frac{7}{12}S_{\triangle NBC}$,$S_{\triangle NBC}=\frac{3}{7}S_{\triangle ABC}$,$S_{\triangle QBC}=\frac{1}{4}S_{\triangle ABC}$,则$S_{\triangle QBC}:S_{\triangle ABC}=1:4$;$\overrightarrow{BP}=\frac{7}{12}\overrightarrow{BM}$,$S_{\triangle PAC}=\frac{5}{12}S_{\triangle BAC}$,$\overrightarrow{BQ}=\frac{7}{12}\overrightarrow{BN}$,$S_{\triangle QAC}=\frac{5}{12}S_{\triangle BAC}$,所以$S_{\triangle PAC}:S_{\triangle QAC}=1:1$,$S_{\triangle QAC}:S_{\triangle ABC}=5:12$.故选ABD.
4. (多选) 生于瑞士的数学巨星欧拉在 1765 年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上.”这就是著名的欧拉线定理.在$\triangle ABC$中,$O,H,G$分别是外心、垂心和重心,$D$为$BC$边的中点,下列四个选项中正确的是 (
A.$\overrightarrow{GH} = 2\overrightarrow{OG}$
B.$\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = 0$
C.$\overrightarrow{AH} = 2\overrightarrow{OD}$
D.$S_{\triangle ABG} = S_{\triangle BCG} = S_{\triangle ACG}$
ABCD
)A.$\overrightarrow{GH} = 2\overrightarrow{OG}$
B.$\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = 0$
C.$\overrightarrow{AH} = 2\overrightarrow{OD}$
D.$S_{\triangle ABG} = S_{\triangle BCG} = S_{\triangle ACG}$
答案:
4.ABCD 在$\triangle ABC$中,$O,H,G$分别是外心、垂心和重心,画出图形,如图所示
对于B选项,根据三角形的重心性质可得$G$为$AD$的三等分点,且$\overrightarrow{GA}=-2\overrightarrow{GD}$,又$D$为$BC$的中点,所以$\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GD}$,所以$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=-2\overrightarrow{GD}+2\overrightarrow{GD}=0$,故选项B正确;
对于A与C选项,因为$O$为$\triangle ABC$的外心,$D$为$BC$的中点,
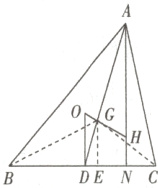
所以$OD\perp BC$,所以$AH// OD$,$\therefore\triangle AHG\sim\triangle DOG$,$\therefore\frac{GH}{OG}=\frac{AH}{OD}=\frac{AG}{DG}=2$,$\therefore GH=2OG$,$AH=2OD$,故选项A、C正确;
对于D,过点$G$作$GE\perp BC$,垂足为$E$,$\therefore\triangle DEG\sim\triangle DNA$,则$\frac{GE}{AN}=\frac{DG}{DA}=\frac{1}{3}$,$\therefore\triangle BGC$的面积为$S_{\triangle BGC}=\frac{1}{2}× BC× GE=\frac{1}{2}× BC×\frac{1}{3}× AN=\frac{1}{3}S_{\triangle ABC}$;同理,$S_{\triangle AGC}=S_{\triangle AGB}=\frac{1}{3}S_{\triangle ABC}$,选项D正确.故选ABCD.
4.ABCD 在$\triangle ABC$中,$O,H,G$分别是外心、垂心和重心,画出图形,如图所示
对于B选项,根据三角形的重心性质可得$G$为$AD$的三等分点,且$\overrightarrow{GA}=-2\overrightarrow{GD}$,又$D$为$BC$的中点,所以$\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GD}$,所以$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=-2\overrightarrow{GD}+2\overrightarrow{GD}=0$,故选项B正确;
对于A与C选项,因为$O$为$\triangle ABC$的外心,$D$为$BC$的中点,

所以$OD\perp BC$,所以$AH// OD$,$\therefore\triangle AHG\sim\triangle DOG$,$\therefore\frac{GH}{OG}=\frac{AH}{OD}=\frac{AG}{DG}=2$,$\therefore GH=2OG$,$AH=2OD$,故选项A、C正确;
对于D,过点$G$作$GE\perp BC$,垂足为$E$,$\therefore\triangle DEG\sim\triangle DNA$,则$\frac{GE}{AN}=\frac{DG}{DA}=\frac{1}{3}$,$\therefore\triangle BGC$的面积为$S_{\triangle BGC}=\frac{1}{2}× BC× GE=\frac{1}{2}× BC×\frac{1}{3}× AN=\frac{1}{3}S_{\triangle ABC}$;同理,$S_{\triangle AGC}=S_{\triangle AGB}=\frac{1}{3}S_{\triangle ABC}$,选项D正确.故选ABCD.
5. 已知在$\triangle ABC$所在的平面内有一点$P$,满足$\overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} = \overrightarrow{AB}$,则$\triangle PBC$与$\triangle ABC$的面积之比是
2:3
.
答案:
5.$2:3$ 因为$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}$,所以$\overrightarrow{PC}=\overrightarrow{AB}-\overrightarrow{PB}-\overrightarrow{PA}=\overrightarrow{AB}+\overrightarrow{BP}+\overrightarrow{AP}=2\overrightarrow{AP}$,所以点$P$在边$CA$上,且是靠近点$A$一侧的三等分点,所以$\triangle PBC$和$\triangle ABC$的面积之比为$2:3$.
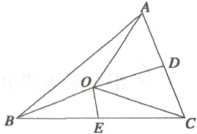
6. 设点$O$在$\triangle ABC$的内部,点$D,E$分别为边$AC,BC$的中点,且$|\overrightarrow{OD} + 2\overrightarrow{OE}| = 1$,则$|\overrightarrow{OA} + 2\overrightarrow{OB} + 3\overrightarrow{OC}| =$
2
.
答案:
6.2 如题图所示,易知$|1\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}|=|1\overrightarrow{OA}+\overrightarrow{OC}+2(\overrightarrow{OB}+\overrightarrow{OC})|=|2\overrightarrow{OD}+4\overrightarrow{OE}|=2|\overrightarrow{OD}+2\overrightarrow{OE}|=2$.
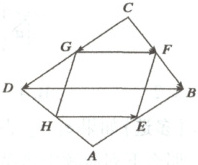
7. 如图,已知$E,F,G,H$分别是四边形$ABCD$的边$AB$、$BC$、$CD$、$DA$的中点,用向量法证明:四边形$EFGH$是平行四边形.

答案:
7.【证明】在$\triangle BCD$中,$\because G,F$分别是$CD,CB$的中点,$\therefore\overrightarrow{CG}=\frac{1}{2}\overrightarrow{CD}$,$\overrightarrow{CF}=\frac{1}{2}\overrightarrow{CB}$.
$\therefore\overrightarrow{GF}=\overrightarrow{CF}-\overrightarrow{CG}=\frac{1}{2}\overrightarrow{CB}-\frac{1}{2}\overrightarrow{CD}=\frac{1}{2}\overrightarrow{DB}$.
同理$\overrightarrow{HE}=\frac{1}{2}\overrightarrow{DB}$.
$\therefore\overrightarrow{GF}=\overrightarrow{HE}$,即$\overrightarrow{GF}$与$\overrightarrow{HE}$共线.
又$\because G,F,H,E$四点不在同一条直线上,$\therefore GF// HE$,且$GF=HE$.
$\therefore$四边形$EFGH$是平行四边形.
$\therefore\overrightarrow{GF}=\overrightarrow{CF}-\overrightarrow{CG}=\frac{1}{2}\overrightarrow{CB}-\frac{1}{2}\overrightarrow{CD}=\frac{1}{2}\overrightarrow{DB}$.
同理$\overrightarrow{HE}=\frac{1}{2}\overrightarrow{DB}$.
$\therefore\overrightarrow{GF}=\overrightarrow{HE}$,即$\overrightarrow{GF}$与$\overrightarrow{HE}$共线.
又$\because G,F,H,E$四点不在同一条直线上,$\therefore GF// HE$,且$GF=HE$.
$\therefore$四边形$EFGH$是平行四边形.
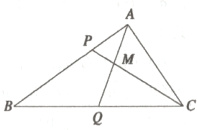
8. 在$\triangle ABC$中,点$P$是$AB$上一点,且$\overrightarrow{CP} = \frac{2}{3}\overrightarrow{CA} + \frac{1}{3}\overrightarrow{CB}$,$Q$是$BC$的中点,$AQ$与$CP$的交点为$M$,且$\overrightarrow{CM} = t\overrightarrow{CP}$,求$t$的值.
答案:
8.$\because\overrightarrow{CP}=\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$,$\therefore3\overrightarrow{CP}=2\overrightarrow{CA}+\overrightarrow{CB}$,即$2\overrightarrow{CP}-2\overrightarrow{CA}=\overrightarrow{CB}-\overrightarrow{CP}$,$\therefore2\overrightarrow{AP}=\overrightarrow{PB}$,即$P$为$AB$的一个三等分点(靠近点$A$),如图所示.
$\because A,M,Q$三点共线,
$\therefore$设$\overrightarrow{CM}=x\overrightarrow{CQ}+(1 - x)\overrightarrow{CA}=\frac{x}{2}\overrightarrow{CB}+(x - 1)\overrightarrow{AC}$,又$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}$,$\therefore\overrightarrow{CM}=\frac{x}{2}\overrightarrow{AB}+(\frac{x}{2}-1)\overrightarrow{AC}$.
又$\overrightarrow{CP}=\overrightarrow{AP}-\overrightarrow{AC}=\frac{1}{3}\overrightarrow{AB}-\overrightarrow{AC}$,$\overrightarrow{CM}=t\overrightarrow{CP}$,$\therefore\frac{x}{2}\overrightarrow{AB}+(\frac{x}{2}-1)\overrightarrow{AC}=t(\frac{1}{3}\overrightarrow{AB}-\overrightarrow{AC})$.
$\therefore\begin{cases}\frac{x}{2}=\frac{t}{3}\frac{x}{2}-1=-t\end{cases}$,解得$t=\frac{3}{4}$
8.$\because\overrightarrow{CP}=\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$,$\therefore3\overrightarrow{CP}=2\overrightarrow{CA}+\overrightarrow{CB}$,即$2\overrightarrow{CP}-2\overrightarrow{CA}=\overrightarrow{CB}-\overrightarrow{CP}$,$\therefore2\overrightarrow{AP}=\overrightarrow{PB}$,即$P$为$AB$的一个三等分点(靠近点$A$),如图所示.
$\because A,M,Q$三点共线,

$\therefore$设$\overrightarrow{CM}=x\overrightarrow{CQ}+(1 - x)\overrightarrow{CA}=\frac{x}{2}\overrightarrow{CB}+(x - 1)\overrightarrow{AC}$,又$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}$,$\therefore\overrightarrow{CM}=\frac{x}{2}\overrightarrow{AB}+(\frac{x}{2}-1)\overrightarrow{AC}$.
又$\overrightarrow{CP}=\overrightarrow{AP}-\overrightarrow{AC}=\frac{1}{3}\overrightarrow{AB}-\overrightarrow{AC}$,$\overrightarrow{CM}=t\overrightarrow{CP}$,$\therefore\frac{x}{2}\overrightarrow{AB}+(\frac{x}{2}-1)\overrightarrow{AC}=t(\frac{1}{3}\overrightarrow{AB}-\overrightarrow{AC})$.
$\therefore\begin{cases}\frac{x}{2}=\frac{t}{3}\frac{x}{2}-1=-t\end{cases}$,解得$t=\frac{3}{4}$
查看更多完整答案,请扫码查看


