2025年成才之路高中新课程学习指导高中数学必修第二册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中数学必修第二册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在平行四边形$ABCD$中,下列结论错误的是(

A.$\overrightarrow{AB} = \overrightarrow{DC}$
B.$\overrightarrow{AD} + \overrightarrow{AB} = \overrightarrow{AC}$
C.$\overrightarrow{AB} - \overrightarrow{AD} = \overrightarrow{BD}$
D.$\overrightarrow{AD} + \overrightarrow{CB} = 0$
C
)
A.$\overrightarrow{AB} = \overrightarrow{DC}$
B.$\overrightarrow{AD} + \overrightarrow{AB} = \overrightarrow{AC}$
C.$\overrightarrow{AB} - \overrightarrow{AD} = \overrightarrow{BD}$
D.$\overrightarrow{AD} + \overrightarrow{CB} = 0$
答案:
1.C A项显然正确,由平行四边形法则知B正确;C项中$\overrightarrow{AB}$ - $\overrightarrow{AD}$ = $\overrightarrow{DB}$,故C错误;D项中$\overrightarrow{AD}$ + $\overrightarrow{CB}$ = $\overrightarrow{AD}$ + $\overrightarrow{DA}$ = 0,故选C。
2. 如图,$D,E,F$是$\triangle ABC$的边$AB,BC,CA$的中点,则$\overrightarrow{AF} - \overrightarrow{DB} =$
(
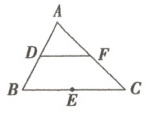
A.$\overrightarrow{FD}$
B.$\overrightarrow{FC}$
C.$\overrightarrow{FE}$
D.$\overrightarrow{BE}$
(
D
)
A.$\overrightarrow{FD}$
B.$\overrightarrow{FC}$
C.$\overrightarrow{FE}$
D.$\overrightarrow{BE}$
答案:
2.D 由图可知,$\overrightarrow{AF}$ - $\overrightarrow{DB}$ = $\overrightarrow{AF}$ - $\overrightarrow{AD}$ = $\overrightarrow{DF}$ = $\overrightarrow{BE}$。
3. 已知$D,E,F$分别是$\triangle ABC$的边$AB,BC,CA$的中点,则
(
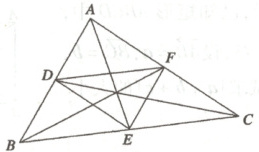
A.$\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} = 0$
B.$\overrightarrow{BD} - \overrightarrow{CF} + \overrightarrow{DF} = 0$
C.$\overrightarrow{AD} + \overrightarrow{CE} - \overrightarrow{CF} = 0$
D.$\overrightarrow{BD} - \overrightarrow{BE} - \overrightarrow{FC} = 0$
(
A
)
A.$\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} = 0$
B.$\overrightarrow{BD} - \overrightarrow{CF} + \overrightarrow{DF} = 0$
C.$\overrightarrow{AD} + \overrightarrow{CE} - \overrightarrow{CF} = 0$
D.$\overrightarrow{BD} - \overrightarrow{BE} - \overrightarrow{FC} = 0$
答案:
3.A
4. 若$D$为$\triangle ABC$的边$BC$的中点,则$\overrightarrow{AC} =$
(
A.$2\overrightarrow{AB} - \overrightarrow{AD}$
B.$2\overrightarrow{AD} - \overrightarrow{AB}$
C.$2\overrightarrow{AD} + \overrightarrow{AB}$
D.$2\overrightarrow{AB} + \overrightarrow{AD}$
(
B
)A.$2\overrightarrow{AB} - \overrightarrow{AD}$
B.$2\overrightarrow{AD} - \overrightarrow{AB}$
C.$2\overrightarrow{AD} + \overrightarrow{AB}$
D.$2\overrightarrow{AB} + \overrightarrow{AD}$
答案:
4.B 因为D为△ABC的边BC的中点,所以,根据向量加法法则得$\overrightarrow{AC}$ + $\overrightarrow{AB}$ = 2$\overrightarrow{AD}$,所以$\overrightarrow{AC}$ = 2$\overrightarrow{AD}$ - $\overrightarrow{AB}$。故选B。

4.B 因为D为△ABC的边BC的中点,所以,根据向量加法法则得$\overrightarrow{AC}$ + $\overrightarrow{AB}$ = 2$\overrightarrow{AD}$,所以$\overrightarrow{AC}$ = 2$\overrightarrow{AD}$ - $\overrightarrow{AB}$。故选B。

5. $O$是四边形$ABCD$所在平面上任一点,$\overrightarrow{AB} // \overrightarrow{CD}$,且$|\overrightarrow{OA} - \overrightarrow{OB}| = |\overrightarrow{OC} - \overrightarrow{OD}|$,则四边形$ABCD$一定为 (
A.菱形
B.任意四边形
C.矩形
D.平行四边形
D
)A.菱形
B.任意四边形
C.矩形
D.平行四边形
答案:
5.D 由$|\overrightarrow{OA} - \overrightarrow{OB}|$ = $|\overrightarrow{OC} - \overrightarrow{OD}|$知$|\overrightarrow{BA}|$ = $|\overrightarrow{DC}|$,且$\overrightarrow{AB}$//$\overrightarrow{CD}$,故四边形ABCD是平行四边形。
6. 已知$\overrightarrow{OA} = a,\overrightarrow{OB} = b,\overrightarrow{OC} = c,\overrightarrow{OD} = d$,且四边形$ABCD$为平行四边形,则
(
A.$a + b + c + d = 0$
B.$a - b + c - d = 0$
C.$a + b - c - d = 0$
D.$a - b - c + d = 0$
(
B
)A.$a + b + c + d = 0$
B.$a - b + c - d = 0$
C.$a + b - c - d = 0$
D.$a - b - c + d = 0$
答案:
6.B 如图,$\boldsymbol{a}$ - $\boldsymbol{b}$ = $\overrightarrow{OA}$ - $\overrightarrow{OB}$ = $\overrightarrow{BA}$,$\boldsymbol{c}$ - $\boldsymbol{d}$ = $\overrightarrow{OC}$ - $\overrightarrow{OD}$ = $\overrightarrow{DC}$,又四边形ABCD为平行四边形,则$\overrightarrow{BA}$ = $\overrightarrow{CD}$,即$\overrightarrow{BA}$ - $\overrightarrow{CD}$ = 0,所以$\overrightarrow{BA}$ + $\overrightarrow{DC}$ = 0,即$\boldsymbol{a}$ - $\boldsymbol{b}$ + $\boldsymbol{c}$ - $\boldsymbol{d}$ = 0。故选B。

6.B 如图,$\boldsymbol{a}$ - $\boldsymbol{b}$ = $\overrightarrow{OA}$ - $\overrightarrow{OB}$ = $\overrightarrow{BA}$,$\boldsymbol{c}$ - $\boldsymbol{d}$ = $\overrightarrow{OC}$ - $\overrightarrow{OD}$ = $\overrightarrow{DC}$,又四边形ABCD为平行四边形,则$\overrightarrow{BA}$ = $\overrightarrow{CD}$,即$\overrightarrow{BA}$ - $\overrightarrow{CD}$ = 0,所以$\overrightarrow{BA}$ + $\overrightarrow{DC}$ = 0,即$\boldsymbol{a}$ - $\boldsymbol{b}$ + $\boldsymbol{c}$ - $\boldsymbol{d}$ = 0。故选B。

7. 如图,已知$O$为平行四边形$ABCD$内一点,$\overrightarrow{OA} = a,\overrightarrow{OB} = b,\overrightarrow{OC} = c$,则$\overrightarrow{OD} =$
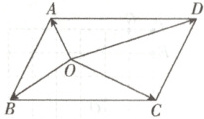
$\boldsymbol{a}$ + $\boldsymbol{c}$ - $\boldsymbol{b}$
.
答案:
7.$\boldsymbol{a}$ + $\boldsymbol{c}$ - $\boldsymbol{b}$ 由已知$\overrightarrow{AD}$ = $\overrightarrow{BC}$,则$\overrightarrow{OD}$ = $\overrightarrow{OA}$ + $\overrightarrow{AD}$ = $\overrightarrow{OA}$ + $\overrightarrow{BC}$ = $\overrightarrow{OA}$ + $\overrightarrow{OC}$ - $\overrightarrow{OB}$ = $\boldsymbol{a}$ + $\boldsymbol{c}$ - $\boldsymbol{b}$。
8. 若向量$a,b$方向相反,且$|a| = |b| = 1$,则$|a - b| =$
2
.
答案:
8.2
9. 如图,在正六边形$ABCDEF$中,与$\overrightarrow{OA} - \overrightarrow{OC} + \overrightarrow{CD}$相等的向量有
$①\overrightarrow{CF};②\overrightarrow{AD};③\overrightarrow{DA};④\overrightarrow{BE};⑤\overrightarrow{CE} + \overrightarrow{BC};⑥\overrightarrow{CA} - \overrightarrow{CD};$
$⑦\overrightarrow{AB} + \overrightarrow{AE}.$

①
.$①\overrightarrow{CF};②\overrightarrow{AD};③\overrightarrow{DA};④\overrightarrow{BE};⑤\overrightarrow{CE} + \overrightarrow{BC};⑥\overrightarrow{CA} - \overrightarrow{CD};$
$⑦\overrightarrow{AB} + \overrightarrow{AE}.$

答案:
9.①$\overrightarrow{OA}$ - $\overrightarrow{OC}$ + $\overrightarrow{CD}$ = $\overrightarrow{CA}$ + $\overrightarrow{CD}$ = $\overrightarrow{CF}$;$\overrightarrow{CE}$ + $\overrightarrow{BC}$ = $\overrightarrow{BC}$ + $\overrightarrow{CE}$ = $\overrightarrow{BE}$ ≠ $\overrightarrow{CF}$;$\overrightarrow{CA}$ - $\overrightarrow{CD}$ = $\overrightarrow{DA}$ ≠ $\overrightarrow{CF}$;$\overrightarrow{AB}$ + $\overrightarrow{AE}$ = $\overrightarrow{AD}$ ≠ $\overrightarrow{CF}$。
10. 如图,在五边形$ABCDE$中,若四边形$ACDE$是平行四边形,且$\overrightarrow{AB} = a,\overrightarrow{AC} = b,\overrightarrow{AE} = c$,试用$a,b,c$表示向量$\overrightarrow{BD},\overrightarrow{BC},\overrightarrow{BE},\overrightarrow{CD}$及$\overrightarrow{CE}$.
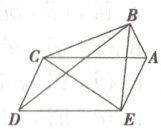

答案:
10.
∵四边形ACDE是平行四边形,
∴$\overrightarrow{CD}$ = $\overrightarrow{AE}$ = $\boldsymbol{c}$,$\overrightarrow{BC}$ = $\overrightarrow{AC}$ - $\overrightarrow{AB}$ = $\boldsymbol{b}$ - $\boldsymbol{a}$,$\overrightarrow{BE}$ = $\overrightarrow{AE}$ - $\overrightarrow{AB}$ = $\boldsymbol{c}$ - $\boldsymbol{a}$,$\overrightarrow{CE}$ = $\overrightarrow{AE}$ - $\overrightarrow{AC}$ = $\boldsymbol{c}$ - $\boldsymbol{b}$,
∴$\overrightarrow{BD}$ = $\overrightarrow{BC}$ + $\overrightarrow{CD}$ = $\boldsymbol{b}$ - $\boldsymbol{a}$ + $\boldsymbol{c}$。
∵四边形ACDE是平行四边形,
∴$\overrightarrow{CD}$ = $\overrightarrow{AE}$ = $\boldsymbol{c}$,$\overrightarrow{BC}$ = $\overrightarrow{AC}$ - $\overrightarrow{AB}$ = $\boldsymbol{b}$ - $\boldsymbol{a}$,$\overrightarrow{BE}$ = $\overrightarrow{AE}$ - $\overrightarrow{AB}$ = $\boldsymbol{c}$ - $\boldsymbol{a}$,$\overrightarrow{CE}$ = $\overrightarrow{AE}$ - $\overrightarrow{AC}$ = $\boldsymbol{c}$ - $\boldsymbol{b}$,
∴$\overrightarrow{BD}$ = $\overrightarrow{BC}$ + $\overrightarrow{CD}$ = $\boldsymbol{b}$ - $\boldsymbol{a}$ + $\boldsymbol{c}$。
查看更多完整答案,请扫码查看


