《2025年单元质量达标七年级数学上册人教版》

9. 用分配律计算$(\frac{1}{4} - \frac{3}{8} - \frac{1}{12})×(-\frac{4}{3})$，去括号正确的是（）

A.$-\frac{1}{4}×\frac{4}{3} - \frac{3}{8} - \frac{1}{12}$
B.$-\frac{1}{4}×\frac{4}{3} - \frac{3}{8}×\frac{4}{3} - \frac{1}{12}×\frac{4}{3}$
C.$-\frac{1}{4}×\frac{4}{3} + \frac{3}{8}×\frac{4}{3} - \frac{1}{12}×\frac{4}{3}$
D.$-\frac{1}{4}×\frac{4}{3} + \frac{3}{8}×\frac{4}{3} + \frac{1}{12}×\frac{4}{3}$

答案： 9.D

10. 如图（1）所示，每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等。按照这个规律，将-1，2，-2，-4，5，-5，6，8填入图（2）中，部分数据已填入，则图中a + b + c - d的值为（）

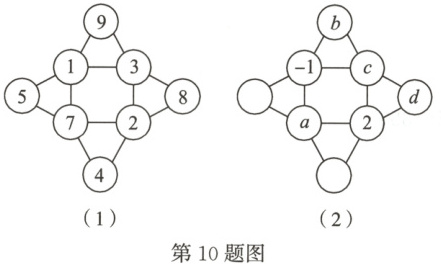
A.4
B.5
C.6
D.7

答案： 10.B

11. 比较大小：$-\frac{4}{5}$$-|-\frac{5}{6}|$。（填“＞”或“＜”）

答案： 11.＞

12. 近似数9.85万精确到位。

答案： 12.百

13. 把（-6） - (-3) + (+1) - (-2)写成省略括号的形式是。

答案： 13.-6+3+1+2

14. 若x，y互为相反数，则$(y + x - 1)^{2024}$ = 。

答案： 14.1

15. 已知x是整数，且-2 ≤ x ＜ 5，则符合条件的所有x值的和为。

答案： 15.7

16. 如果a = -4，那么代数式$(a - \frac{4}{a})·\frac{a^{2}}{a + 3}$的值为。

答案： 16.48

17. 如图，在数轴原点O的右侧，一个小球P从距原点32个单位长度的点A处向原点方向跳动，第一次跳动到OA的中点$A_{1}$处，第二次从$A_{1}$点跳动到$OA_{1}$的中点$A_{2}$处，第三次从$A_{2}$点跳动到$OA_{2}$的中点$A_{3}$处……如此跳动下去，则第六次跳动后，该小球P到原点O的距离为。

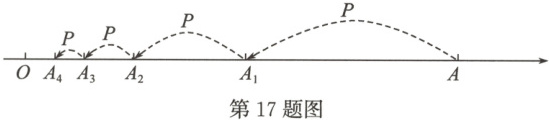
答案： 17.$\frac{1}{2}$

18. 观察下列等式：①2 + $2^{2}$ = $2^{3}$ - 2；②2 + $2^{2}$ + $2^{3}$ = $2^{4}$ - 2；③2 + $2^{2}$ + $2^{3}$ + $2^{4}$ = $2^{5}$ - 2……利用你发现的规律，求$2^{50}$ + $2^{51}$ + $2^{52}$ + … + $2^{99}$的值为。（结果保留幂的形式）
三、解答题（共66分）

答案： 18.$2^{100}-2^{50}$