2025年小题狂做高中数学必修第一册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学必修第一册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
8. 以下式子符号为正的有
(
A.$\tan 108° · \cos 305°$
B.$\frac{\cos\frac{5\pi}{6}· \tan\frac{11\pi}{6}}{\sin\frac{2\pi}{3}}$
C.$\tan 191°-\cos 191°$
D.$\sin 3· \cos 4· \tan 5$
(
BCD
)A.$\tan 108° · \cos 305°$
B.$\frac{\cos\frac{5\pi}{6}· \tan\frac{11\pi}{6}}{\sin\frac{2\pi}{3}}$
C.$\tan 191°-\cos 191°$
D.$\sin 3· \cos 4· \tan 5$
答案:
8. BCD 对于$A$,因为$108^{\circ}$角是第二象限角,所以$\tan108^{\circ}<0$,又$305^{\circ}$角是第四象限角,所以$\cos305^{\circ}>0$,所以$\tan108^{\circ}·\cos305^{\circ}<0$,所以$A$不正确.对于$B$,因为角$\frac{5\pi}{6}$是第二象限角,角$\frac{11\pi}{6}$是第四象限角,角$\frac{2\pi}{3}$是第二象限角,所以$\cos\frac{5\pi}{6}<0,\tan\frac{11\pi}{6}<0,\sin\frac{2\pi}{3}>0$,从而$\frac{\cos\frac{5\pi}{6}·\tan\frac{11\pi}{6}}{\sin\frac{2\pi}{3}}<0$,所以$B$正确.对于$C$,因为$191^{\circ}$角是第三象限角,所以$\tan191^{\circ}>0,\cos191^{\circ}<0$,所以$\tan191^{\circ}-\cos191^{\circ}>0$,所以$C$正确.对于$D$,因为$\frac{\pi}{2}<3<\pi,\pi<4<\frac{3\pi}{2}$,所以$\sin3>0,\cos4<0,\tan5<0$,所以$\sin3·\cos4·\tan5>0$,所以$D$正确.
方法总结 判断三角函数值的正负的关键在于确定角所在的位置,为此,就需要熟练地掌握各个三角函数值在每个象限以及坐标轴上的符号.
方法总结 判断三角函数值的正负的关键在于确定角所在的位置,为此,就需要熟练地掌握各个三角函数值在每个象限以及坐标轴上的符号.
9. 如图,在平面直角坐标系中,圆$O$与$x$轴的正半轴相交于点$A(1,0)$,过点$T(x_0,\sin x_0)$作$x$轴的平行线与圆$O$相交于不同的$B,C$两点,且点$B$在点$C$左侧,设$B(x_1,y_1),C(x_2,y_2)$,下列说法正确的是
(
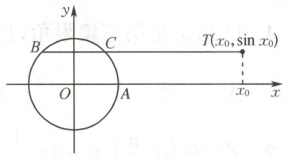
A.若$x_0=\frac{2\pi}{3}$,则$x_1=-\frac{1}{2}$
B.若$x_0=\frac{2\pi}{3}$,则$y_2=\frac{\sqrt{3}}{2}$
C.若$x_1=-\frac{1}{2}$,则$\cos x_0=\frac{1}{2}$
D.若$x_2=\frac{1}{2}$,则$\sin x_0=\frac{1}{2}$
(
AB
)
A.若$x_0=\frac{2\pi}{3}$,则$x_1=-\frac{1}{2}$
B.若$x_0=\frac{2\pi}{3}$,则$y_2=\frac{\sqrt{3}}{2}$
C.若$x_1=-\frac{1}{2}$,则$\cos x_0=\frac{1}{2}$
D.若$x_2=\frac{1}{2}$,则$\sin x_0=\frac{1}{2}$
答案:
9. AB 由题意可知$y_1 = y_2=\sin x_0$.若$x_0=\frac{2\pi}{3}$,则$y_1 = y_2=\sin\frac{2\pi}{3}=\frac{\sqrt{3}}{2}$,则$x_1=-\sqrt{1 - y^2}=-\frac{1}{2}$,故$A,B$正确;若$x_1=-\frac{1}{2}$,则$y_1=\sin x_0=\pm\frac{\sqrt{3}}{2},\cos x_0=\pm\frac{1}{2}$,故$C$错误;若$x_2=\frac{1}{2}$,则$y_2=\sin x_0=\pm\sqrt{1 - x^2}=\pm\frac{\sqrt{3}}{2}$,故$D$错误.
10. 已知角$\alpha$的终边过点$P(m,2)$,且$\cos \alpha=\frac{\sqrt{5}m}{5}$,则$m$的值为
0,±1
.
答案:
10. $0,\pm1$ 根据三角函数的定义可得$\cos\alpha=\frac{m}{\sqrt{m^2 + 2^2}}=\frac{\sqrt{5}m}{5}$,所以$m = 0$或$m^2+2^2 = 5$,即$m = 0$或$\pm1$,故$m$的值为$0,\pm1$.
11. 当角$\alpha$的终边经过点$(\cos\frac{\pi}{3},\sin\frac{\pi}{3})$时,角$\alpha=$
$2k\pi+\frac{\pi}{3}(k\in\mathbf{Z})$
(用弧度制表示);当角$\alpha$的终边经过点$(a,2a),a\neq0$时,$\cos \alpha=$$\pm\frac{\sqrt{5}}{5}$
.
答案:
11. $2k\pi+\frac{\pi}{3}(k\in\mathbf{Z})\pm\frac{\sqrt{5}}{5}$ 因为$\cos\frac{\pi}{3}=\frac{1}{2},\sin\frac{\pi}{3}=\frac{\sqrt{3}}{2}$,所以角$\alpha$的终边与$\frac{\pi}{3}$的终边相同,所以角$\alpha = 2k\pi+\frac{\pi}{3},k\in\mathbf{Z}$.当角$\alpha$的终边经过点$(a,2a),a\neq0$时,若$a>0$,则$\cos\alpha=\frac{\sqrt{5}}{5}$;若$a<0$,则$\cos\alpha=-\frac{\sqrt{5}}{5}$.
12. 如图,单位圆被点$A_1,A_2,·s,A_{12}$分为12等份,其中$A_1(1,0)$. 角$\alpha$的始边与$x$轴的非负半轴重合,若$\alpha$的终边经过点$A_5$,则$\cos \alpha=$
$-\frac{1}{2}$
;若$\tan \alpha=\sqrt{3}$,则角$\alpha$的终边与单位圆交于点$A_3,A_9$
(从$A_1,A_2,·s,A_{12}$中选择,写出所有满足要求的点).
答案:
12. $-\frac{1}{2}A_3,A_9$ 因为$\frac{2\pi}{12}=\frac{\pi}{6}$,所以若角$\alpha$的终边经过$A_i$,则$\alpha=(i - 1)\frac{\pi}{6}(1\leq i\leq12,i\in\mathbf{Z})$.角$\alpha$的始边与$x$轴的非负半轴重合,角$\alpha$的终边经过点$A_5$,则$\alpha=\frac{2\pi}{3}$,所以$\cos\alpha=\cos\frac{2\pi}{3}=-\frac{1}{2}$.因为$\tan\alpha=\sqrt{3}$,则$\alpha=\frac{\pi}{3}$或$\alpha=\frac{4\pi}{3}$,即$\frac{\pi}{3}=(i - 1)\frac{\pi}{6}(1\leq i\leq12,i\in\mathbf{Z})$或$\frac{4\pi}{3}=(i - 1)\frac{\pi}{6}(1\leq i\leq12,i\in\mathbf{Z})$,得$i = 3$或$9$.所以角$\alpha$经过点$A_3,A_9$.
13. 已知$\frac{1}{|\sin \alpha|}=-\frac{1}{\sin \alpha}$,且$\lg(\cos \alpha)$有意义.
(1) 试判断角$\alpha$所在的象限;
(2) 若角$\alpha$的终边与单位圆相交于点$M(\frac{3}{5},m)$,求$m$的值及$\sin \alpha$的值.
(1) 试判断角$\alpha$所在的象限;
(2) 若角$\alpha$的终边与单位圆相交于点$M(\frac{3}{5},m)$,求$m$的值及$\sin \alpha$的值.
答案:
13. 解:
(1)因为$\frac{1}{|\sin\alpha|}=-\frac{1}{\sin\alpha}$,所以$\sin\alpha<0$ ①,由$\lg(\cos\alpha)$有意义,得$\cos\alpha>0$ ②,由①②得角$\alpha$在第四象限.
(2)因为点$M(\frac{3}{5},m)$在单位圆上,所以$(\frac{3}{5})^2+m^2 = 1$,解得$m=\pm\frac{4}{5}$.又$\alpha$是第四象限角,所以$m<0$,所以$m = -\frac{4}{5}$.由三角函数定义知$\sin\alpha=-\frac{4}{5}$.
(1)因为$\frac{1}{|\sin\alpha|}=-\frac{1}{\sin\alpha}$,所以$\sin\alpha<0$ ①,由$\lg(\cos\alpha)$有意义,得$\cos\alpha>0$ ②,由①②得角$\alpha$在第四象限.
(2)因为点$M(\frac{3}{5},m)$在单位圆上,所以$(\frac{3}{5})^2+m^2 = 1$,解得$m=\pm\frac{4}{5}$.又$\alpha$是第四象限角,所以$m<0$,所以$m = -\frac{4}{5}$.由三角函数定义知$\sin\alpha=-\frac{4}{5}$.
如图,动点$P,Q$从点$A(4,0)$出发,沿圆周运动,点$P$按逆时针方向每秒钟转$\frac{\pi}{3} rad$,点$Q$按顺时针方向每秒钟转$\frac{\pi}{6} rad$,求$P,Q$第一次相遇时所用的时间、相遇点的坐标及$P,Q$两点各自走过的弧长.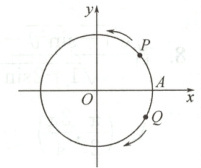

答案:
[探究拓展] 解:设$P,Q$第一次相遇时所用的时间是$t$秒,则$t·\frac{\pi}{3}+t·|-\frac{\pi}{6}| = 2\pi$,所以$t = 4$(秒),即第一次相遇的时间为$4$秒.设第一次相遇点为$C$,第一次相遇时点$P$已运动到终边在$\frac{\pi}{3}·4=\frac{4\pi}{3}$的位置,则$x_C=\cos\frac{4\pi}{3}×4=-2,y_C=\sin\frac{4\pi}{3}×4=-2\sqrt{3}$.所以点$C$的坐标为$(-2,-2\sqrt{3})$,点$P$走过的弧长为$\frac{4\pi}{3}×4=\frac{16\pi}{3}$,点$Q$走过的弧长为$\frac{2\pi}{3}×4=\frac{8\pi}{3}$.
核心笔记
1. 任意角的三角函数的定义是三角函数的基础内容,对它的学习要注意以下方面:
(1)利用三角函数的定义求三角函数值;(第 1,2,3,10 题)
(2)判断各个三角函数值在各个象限及坐标轴上的符号;(第 4,7,13
(1)题)
(3)求特殊角的三角函数值或根据特殊的三角函数值求角.(第 3,11 题)
2. 单位圆中的三角函数线是三角函数定义的体现,是三角函数值的几何表示,为此,要能应用它来解决一些基本问题:
(1)解三角不等式;(第 5 题)
(2)比较三角函数值的大小或根据三角函数值的大小判断角的范围.
高中数学小题狂做·必修第一册·SJ
3. 根据角的终边上的点的坐标关系求角的大小.
核心笔记
1. 任意角的三角函数的定义是三角函数的基础内容,对它的学习要注意以下方面:
(1)利用三角函数的定义求三角函数值;(第 1,2,3,10 题)
(2)判断各个三角函数值在各个象限及坐标轴上的符号;(第 4,7,13
(1)题)
(3)求特殊角的三角函数值或根据特殊的三角函数值求角.(第 3,11 题)
2. 单位圆中的三角函数线是三角函数定义的体现,是三角函数值的几何表示,为此,要能应用它来解决一些基本问题:
(1)解三角不等式;(第 5 题)
(2)比较三角函数值的大小或根据三角函数值的大小判断角的范围.
高中数学小题狂做·必修第一册·SJ
3. 根据角的终边上的点的坐标关系求角的大小.
查看更多完整答案,请扫码查看


