《2025年小题狂做高中数学选择性必修第二册苏教版》

1. （2024 广东阶段练习）如图，已知正方体$ABCD - A_1B_1C_1D_1$的中心为$O$，则下列结论正确的是 $\boldsymbol{(\quad)}$


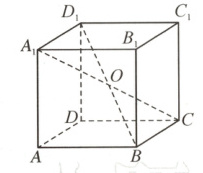
$A.\overrightarrow{OA} + \overrightarrow{OD}$与$\overrightarrow{OA_1} + \overrightarrow{OD_1}$是一对相反向量
$B.\overrightarrow{OB} - \overrightarrow{OC_1}$与$\overrightarrow{OC} - \overrightarrow{OB_1}$是一对相反向量
$C.\overrightarrow{OA_1} + \overrightarrow{OB_1} + \overrightarrow{OC_1} + \overrightarrow{OD_1}$与$\overrightarrow{OD} + \overrightarrow{OC} + \overrightarrow{OB} + \overrightarrow{OA}$是一对相反向量
$D.\overrightarrow{OC} - \overrightarrow{OA}$与$\overrightarrow{OC_1} - \overrightarrow{OA_1}$是一对相反向量

答案：
1.C设E,F分别为AD和A₁D₁的中点.对于A，$\overrightarrow{OA} + \overrightarrow{OD} = 2\overrightarrow{OE}$与$\overrightarrow{OA₁} + \overrightarrow{OD₁} = 2\overrightarrow{OF}$不是一对相反向量，错误；对于B，$\overrightarrow{OB} - \overrightarrow{OC} = \overrightarrow{CB}$与$\overrightarrow{OC} - \overrightarrow{OB} = \overrightarrow{B₁C₁}$不是一对相反向量，错误；对于C，$\overrightarrow{OA₁} + \overrightarrow{OB₁} + \overrightarrow{OC₁} + \overrightarrow{OD₁} = - \overrightarrow{OC} - \overrightarrow{OD} - \overrightarrow{OA} - \overrightarrow{OB} = - (\overrightarrow{OC} + \overrightarrow{OD} + \overrightarrow{OA} + \overrightarrow{OB})$与$\overrightarrow{OD₁} + \overrightarrow{OC₁} + \overrightarrow{OA₁} + \overrightarrow{OB₁}$是一对相反向量，正确；对于D，$\overrightarrow{OC₁} - \overrightarrow{OA} = \overrightarrow{AC₁}$与$\overrightarrow{OC₁} - \overrightarrow{OA₁} = \overrightarrow{A₁C₁}$不是一对相反向量，是一对相等向量，错误.

2. （2024 安徽亳州阶段检测）在长方体$ABCD - A_1B_1C_1D_1$中，$O$为线段$AC$的中点，则$\overrightarrow{OA_1} + \overrightarrow{AD} + \overrightarrow{AB} = \boldsymbol{(\quad)}$

A.$\overrightarrow{AD_1}$
B.$\overrightarrow{OB_1}$
C.$\overrightarrow{OC_1}$
D.$\overrightarrow{OD_1}$

答案： 2.C因为O为线段AC的中点，所以$\overrightarrow{AB} + \overrightarrow{AD} = 2\overrightarrow{AO}$，所以$\overrightarrow{OA} + \overrightarrow{AD} + \overrightarrow{AB} = 2\overrightarrow{AO} + \overrightarrow{OA} = \overrightarrow{AO} + \overrightarrow{AA₁}$。因为在长方体ABCD - A₁B₁C₁D₁中，$\overrightarrow{AO} = \overrightarrow{OC}$，$\overrightarrow{AA₁} = \overrightarrow{CC₁}$，所以$\overrightarrow{AO} + \overrightarrow{AA₁} = \overrightarrow{OC} + \overrightarrow{CC₁} = \overrightarrow{OC₁}$，即$\overrightarrow{OA} + \overrightarrow{AD} + \overrightarrow{AB} = \overrightarrow{OC₁}$。
方法总结：空间向量加法、减法运算的两个技巧
(1)巧用相反向量：向量的三角形法则是解决空间向量加法、减法运算的关键，灵活运用相反向量可使向量首尾相接。
(2)巧用平移：利用三角形法则和平行四边形法则进行向量加、减法运算时，务必注意和向量、差向量的方向，必要时可采用空间向量的自由平移获得运算结果。

$3. （2024 $江苏淮安联考$）$已知空间四边形$ABCD，$$E，$$F$分别是边$AB$与$AD$上的点，$M，$$N$分别是边$BC$与$CD$上的点。若$\overrightarrow{AE} = \lambda\overrightarrow{AB}，$$\overrightarrow{AF} = \lambda\overrightarrow{AD}，$$\overrightarrow{CM} = \mu\overrightarrow{CB}，$$\overrightarrow{CN} = \mu\overrightarrow{CD}，$则向量$\overrightarrow{EF}$与$\overrightarrow{MN}$满足的关系为$ \boldsymbol{(\quad)}$　　

A.$\overrightarrow{EF} = \overrightarrow{MN}$
B.$\overrightarrow{EF} // \overrightarrow{MN}$
C.$|\overrightarrow{EF}| = |\overrightarrow{MN}|$
D.$|\overrightarrow{EF}| \neq |\overrightarrow{MN}|$

答案： 3.B由$\overrightarrow{AE} = \lambda\overrightarrow{AB}$，$\overrightarrow{AF} = \lambda\overrightarrow{AD}$，得$\overrightarrow{EF} = \overrightarrow{AF} - \overrightarrow{AE} = \lambda(\overrightarrow{AD} - \overrightarrow{AB}) = \lambda\overrightarrow{BD}$，所以$\overrightarrow{EF}$，$\overrightarrow{BD}$共线，同理，由$\overrightarrow{CM} = \mu\overrightarrow{CB}$，$\overrightarrow{CN} = \mu\overrightarrow{CD}$，得$\overrightarrow{MN} = \mu\overrightarrow{BD}$，所以$\overrightarrow{MN}$，$\overrightarrow{BD}$共线，所以$\overrightarrow{EF}$，$\overrightarrow{MN}$共线，即EF//MN。
方法总结：向量共线的判定及应用：判断或证明两向量$\vec{a}$，$\vec{b}$（$\vec{a} \neq 0$）共线，就是寻找实数$\lambda$，使$\vec{b} = \lambda\vec{a}$成立。

4. （多选题，2024 四川期中）下列说法正确的是 $\boldsymbol{(\quad)}$

A.零向量没有方向
B.空间向量不能比较大小，空间向量的模可以比较大小
C.如果两个向量不相同，那么它们的长度不相等
D.同向且等长的有向线段表示同一向量

答案： 4.BD对于A，零向量的方向是任意的，A错误；B正确；对于C，D，长度相等、方向相同的两个向量为相等向量，即同一向量，所以C中向量长度可以相等，只要方向不同即为不同向量，C错误；D符合定义，D正确。
方法总结：
(1)判断有关向量的命题时，要抓住向量的两个主要元素，即长度和方向，两者缺一不可。
(2)要注意零向量的特殊性。对于零向量，我们应明确：
①零向量不是没有方向，它的方向是任意的；
②零向量与任何向量都共线。
(3)在空间中，向量、向量的模、相等向量的概念和平面中向量的相关概念完全一致。两个向量相等的充要条件是两个向量的方向相同、模相等。两个向量互为相反向量的充要条件是模相等、方向相反。

5. (2024 江西景德镇期末)在空间四边形$OABC$中,化简$\overrightarrow{OA}+\overrightarrow{AB}-\overrightarrow{CB}=$____.

答案： 5.$\overrightarrow{OC}$ $\overrightarrow{OA} + \overrightarrow{AB} - \overrightarrow{CB} = \overrightarrow{OB} - \overrightarrow{CB} = \overrightarrow{BC} - \overrightarrow{BO} = \overrightarrow{OC}$。

6. (2024 上海浦东阶段检测)设$\boldsymbol{e_1}，$$\boldsymbol{e_2}$是空间两个不共线的非零向量，已知$\overrightarrow{AB} = 2\boldsymbol{e_1} + k\boldsymbol{e_2}，$$\overrightarrow{BC} = \boldsymbol{e_1} + 3\boldsymbol{e_2}，$$\overrightarrow{DC} = 2\boldsymbol{e_1} - \boldsymbol{e_2}，$且A，B，D三点共线，则实数k的值为-8。

答案： 6.-8因为$\overrightarrow{BC} = \vec{e₁} + 3\vec{e₂}$，$\overrightarrow{DC} = 2\vec{e₁} - \vec{e₂}$，所以$\overrightarrow{BD} = \overrightarrow{BC} + \overrightarrow{CD} = (\vec{e₁} + 3\vec{e₂}) - (2\vec{e₁} - \vec{e₂}) = - \vec{e₁} + 4\vec{e₂}$。又因为A，B，D三点共线，所以可设$\overrightarrow{AB} = \lambda\overrightarrow{BD}$，即$2\vec{e₁} + k\vec{e₂} = \lambda(- \vec{e₁} + 4\vec{e₂})$。因为$\vec{e₁}$，$\vec{e₂}$不共线，所以$\begin{cases} 2 = - \lambda, \\ k = 4\lambda, \end{cases}$解得$k = - 8$。
方法总结：A，B，C三点共线⇔存在实数$\lambda$，使$\overrightarrow{AB} = \lambda\overrightarrow{BC}$或$\overrightarrow{AB} = \lambda\overrightarrow{AC}$。

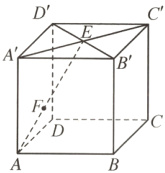
7. （2024 辽宁沈阳阶段检测）已知正方体$ABCD - A'B'C'D'$，$E$是$A'C'$的中点，$F$是$AE$的三等分点，且$AF = \frac{1}{2}EF$，则$\overrightarrow{AF} = \boldsymbol{(\quad)}$

A.$\overrightarrow{AA'} + \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AD}$
B.$\frac{1}{2}\overrightarrow{AA'} + \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AD}$
C.$\frac{1}{2}\overrightarrow{AA'} + \frac{1}{6}\overrightarrow{AB} + \frac{1}{6}\overrightarrow{AD}$
D.$\frac{1}{3}\overrightarrow{AA'} + \frac{1}{6}\overrightarrow{AB} + \frac{1}{6}\overrightarrow{AD}$

答案：
7.D如图所示，由于AF = $\frac{1}{2}$EF，故$\overrightarrow{AF} = \frac{1}{3}\overrightarrow{AE}$。又$\overrightarrow{AE} = \overrightarrow{AA₁} + \overrightarrow{A₁E}$，$\overrightarrow{A₁E} = \frac{1}{2}\overrightarrow{A₁C₁}$，$\overrightarrow{A₁C₁} = \overrightarrow{A₁D₁} + \overrightarrow{A₁B₁}$，$\overrightarrow{A₁D₁} = \overrightarrow{AD}$，$\overrightarrow{A₁B₁} = \overrightarrow{AB}$，所以$\overrightarrow{AF} = \frac{1}{3}\overrightarrow{AE} = \frac{1}{3}(\overrightarrow{AA₁} + \frac{1}{2}\overrightarrow{A₁C₁}) = \frac{1}{3}\overrightarrow{AA₁} + \frac{1}{6}(\overrightarrow{A₁B₁} + \overrightarrow{A₁D₁}) = \frac{1}{3}\overrightarrow{AA₁} + \frac{1}{6}(\overrightarrow{AB} + \overrightarrow{AD}) = \frac{1}{3}\overrightarrow{AA₁} + \frac{1}{6}\overrightarrow{AB} + \frac{1}{6}\overrightarrow{AD}$。

方法总结：
(1)利用数乘运算进行向量表示的注意点：
①数形结合：利用数乘运算解题时，要结合具体图形，利用三角形法则、平行四边形法则，将目标向量转化为已知向量。
②明确目标：在化简过程中要有目标意识，巧妙利用线段的中点进行解题。
(2)进行向量的线性运算，实质上是在正确运用数乘运算律的基础上进行向量求和，即通过作出向量，运用平行四边形法则或三角形法则求和。运算的关键是将相应的向量放到同一个三角形或平行四边形中。

8. （2024 福建莆田阶段练习）已知不共线向量$\boldsymbol{e_1}，$$\boldsymbol{e_2}，$$\boldsymbol{e_3}，$$\overrightarrow{OP} = \boldsymbol{e_1} - 2\boldsymbol{e_2} + \boldsymbol{e_3}，$$\overrightarrow{PQ} = -5\boldsymbol{e_1} - \boldsymbol{6e_2} + 4\boldsymbol{e_3}，$$\overrightarrow{QR} = 7\boldsymbol{e_1} + 2\boldsymbol{e_2} - 2\boldsymbol{e_3}，$则一定共线的三个点是$ \boldsymbol{(\quad)}$

A.O，P，Q
B.P，Q，R
C.O，Q，R
D.O，P，R

答案： 8.D若$\overrightarrow{OP} // \overrightarrow{PQ}$，则存在唯一实数$\lambda$，使得$\overrightarrow{OP} = \lambda\overrightarrow{PQ}$，即$\vec{e₁} - 2\vec{e₂} + \vec{e₃} = \lambda(- 5\vec{e₁} - 6\vec{e₂} + 4\vec{e₃})$，所以$\begin{cases} 1 = - 5\lambda, \\ - 2 = - 6\lambda, \\ 1 = 4\lambda, \end{cases}$无解，所以$\overrightarrow{OP}$，$\overrightarrow{PQ}$不共线，则O，P，Q三点不共线，故A错误；若$\overrightarrow{QR} // \overrightarrow{PQ}$，则存在唯一实数$\lambda$，使得$\overrightarrow{QR} = \lambda\overrightarrow{PQ}$，即$7\vec{e₁} + 2\vec{e₂} - 2\vec{e₃} = \lambda(- 5\vec{e₁} - 6\vec{e₂} + 4\vec{e₃})$，所以$\begin{cases} 7 = - 5\lambda, \\ 2 = - 6\lambda, \\ - 2 = 4\lambda, \end{cases}$无解，所以$\overrightarrow{QR}$，$\overrightarrow{PQ}$不共线，则P，Q，R三点不共线；$\overrightarrow{OQ} = \overrightarrow{OP} + \overrightarrow{PQ} = - 4\vec{e₁} - 8\vec{e₂} + 5\vec{e₃}$，若$\overrightarrow{OQ} // \overrightarrow{QR}$，则存在唯一实数$\lambda$，使得$\overrightarrow{OQ} = \lambda\overrightarrow{QR}$，即$- 4\vec{e₁} - 8\vec{e₂} + 5\vec{e₃} = \lambda(7\vec{e₁} + 2\vec{e₂} - 2\vec{e₃})$，所以$\begin{cases} - 4 = 7\lambda, \\ - 8 = 2\lambda, \\ 5 = - 2\lambda, \end{cases}$无解，所以$\overrightarrow{OQ}$，$\overrightarrow{QR}$不共线，则O，Q，R三点不共线，故C错误；$\overrightarrow{PR} = \overrightarrow{PQ} + \overrightarrow{QR} = 2\vec{e₁} - 4\vec{e₂} + 2\vec{e₃} = 2\overrightarrow{OP}$，所以$\overrightarrow{OP} // \overrightarrow{PR}$，又P为两向量的公共端点，所以O，P，R三点共线，故D正确。