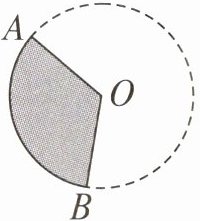
1. 右图中,圆上A、B两点之间的部分叫作(
弧
),读作“(弧AB
)”。一条弧和经过这条弧两端的两条半径所围成的图形叫作(扇形
)。像∠AOB这样,顶点在圆心的角叫作(圆心角
)。
答案:
弧 弧AB 扇形 圆心角
2. 一个扇形的面积是它所在圆的面积的$\frac{1}{3}$,这个扇形的圆心角是(
120
)度。
答案:
120
1. 下面各图中有圆心角的是(

B
)。
答案:
B
2. 用半径相等的扇形拼圆,下面(
A.4个圆心角是$90^{\circ}$的扇形
B.9个圆心角是$36^{\circ}$的扇形
C.6个圆心角是$60^{\circ}$的扇形
D.2个圆心角是$180^{\circ}$的扇形
B
)不可能拼成一个圆。A.4个圆心角是$90^{\circ}$的扇形
B.9个圆心角是$36^{\circ}$的扇形
C.6个圆心角是$60^{\circ}$的扇形
D.2个圆心角是$180^{\circ}$的扇形
答案:
B
3. 把一个圆平均分成偶数等份个小扇形,拼成近似的长方形,长方形的周长比圆周长多6 cm。这个圆的面积是(
A.$3\pi$
B.$6\pi$
C.$12\pi$
D.$9\pi$
D
)$cm^{2}$。A.$3\pi$
B.$6\pi$
C.$12\pi$
D.$9\pi$
答案:
D
三、画一画。
画一个半径是1厘米的圆,再在圆中画一个圆心角是$60^{\circ}$的扇形。
画一个半径是1厘米的圆,再在圆中画一个圆心角是$60^{\circ}$的扇形。
答案:
答题卡作答:
1. 使用圆规,固定圆规两脚间距为1厘米,一脚固定作为圆心O,旋转另一脚画圆。
2. 使用量角器,以圆心O为顶点,在圆内测量并标记出60°的圆心角(如从正右方水平方向开始,向逆时针方向量60°)。
3. 用直尺连接圆心O与60°角对应的圆上的两点A、B。
4. 用弧线连接A、B两点(该弧线为圆周上的一段),形成扇形OAB。
1. 使用圆规,固定圆规两脚间距为1厘米,一脚固定作为圆心O,旋转另一脚画圆。
2. 使用量角器,以圆心O为顶点,在圆内测量并标记出60°的圆心角(如从正右方水平方向开始,向逆时针方向量60°)。
3. 用直尺连接圆心O与60°角对应的圆上的两点A、B。
4. 用弧线连接A、B两点(该弧线为圆周上的一段),形成扇形OAB。
1. 一个钟表的分针长12 cm,当它转动一周时,分针扫过的面积是多少平方厘米?经过45分钟后,分针扫过的面积又是多少呢?
答案:
3.14×12²=452.16(cm²)
452.16×$\frac{3}{4}$=339.12(cm²)
452.16×$\frac{3}{4}$=339.12(cm²)
2. 如图,正方形的周长是16 cm,在正方形里画一个最大的扇形。阴影部分的面积是多少平方厘米?


答案:
16÷4=4(cm)
4²-3.14×4²÷4=3.44(cm²)
4²-3.14×4²÷4=3.44(cm²)
五、培优园。
下面三个正方形的边长都是4 cm,阴影部分的面积相等吗?为什么?

下面三个正方形的边长都是4 cm,阴影部分的面积相等吗?为什么?

答案:
相等,因为阴影部分的面积都等于正方形的面积减去一个半径为2 cm的圆的面积。
$4×\frac{7}{18}=$
$\frac{5}{4}×\frac{4}{15}=$
$\frac{14}{9}$
$36×\frac{3}{9}=$12
$56×\frac{5}{8}=$35
$\frac{5}{6}×54=$45
$\frac{5}{4}×\frac{4}{15}=$
$\frac{1}{3}$
$\frac{27}{32}×\frac{8}{9}=$$\frac{3}{4}$
$\frac{7}{12}÷\frac{7}{24}=$2
$\frac{3}{4}÷\frac{4}{3}=$$\frac{9}{16}$
答案:
$\frac{14}{9}$ 12 35 45 $\frac{1}{3}$ $\frac{3}{4}$ 2 $\frac{9}{16}$
查看更多完整答案,请扫码查看


