《2025年新课程学习与测评同步学习六年级数学上册人教版》

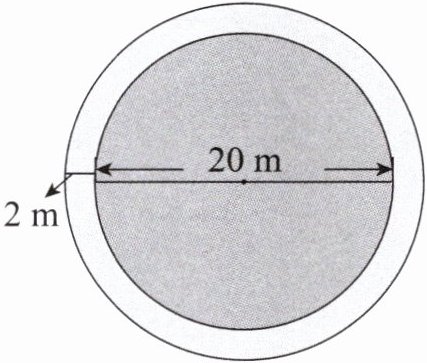
3. 动物园里有一个直径为20m的圆形人工湖,在湖的周围有一条宽为2m的小路,这条小路的面积是多少平方米？

答案： 内圆半径：$20÷2=10$（m），
外圆半径：$10 + 2=12$（m），
圆环面积公式为$S = \pi(R^2 - r^2)$，
$S = 3.14×(12^{2}-10^{2})$
$= 3.14×(144 - 100)$
$= 3.14×44$
$= 138.16$（$m^{2}$）
答：这条小路的面积是$138.16$平方米。

4. 一种圆形标志牌,它的直径是4dm。现在有一块长20dm、宽10dm的长方形铁板,用来做这种圆形标志牌。这块铁板最多可以做多少块标志牌？

答案： 1. 圆形标志牌直径：4dm
2. 长方形铁板长：20dm，宽：10dm
3. 长能容纳的个数：20÷4=5（个）
4. 宽能容纳的个数：10÷4=2（个）……2dm
5. 最多可做个数：5×2=10（块）
答：这块铁板最多可以做10块标志牌。

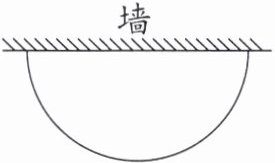
5. 如下图所示,王大妈靠墙用栅栏围了一个半圆形花坛,栅栏长12.56m。这个花坛的面积是多少平方米？

答案： 解：因为靠墙围成半圆形花坛，栅栏长为半圆的弧长。
设半圆的半径为$r$，半圆的弧长公式为$\pi r$。
已知弧长为$12.56m$，则$\pi r = 12.56$，$r = 12.56÷3.14 = 4m$。
半圆的面积公式为$\frac{1}{2}\pi r^2$，则面积为$\frac{1}{2}×3.14×4^2=\frac{1}{2}×3.14×16 = 25.12m^2$。
答：这个花坛的面积是$25.12$平方米。

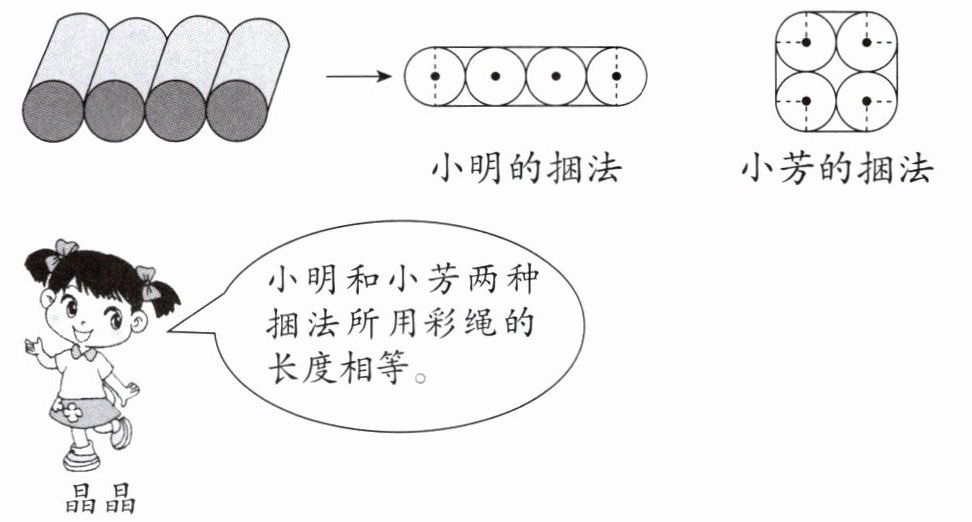
6. 学校开展“卫生纸芯变废为宝”活动。小明和小芳都想到了用纸芯做笔筒,他们分别把4个纸芯摆好后用彩绳捆绑固定,打捆方式如下图所示(打结处彩绳长度不计),已知纸芯的直径约为3cm(纸芯厚度忽略不计)。请你判断晶晶的说法是否正确,并说明理由。

答案： 晶晶的说法不正确，理由如下：
小明的捆法（4个纸芯排成一行）：
彩绳长度=直线部分+曲线部分。
直线部分：上下两条切线，每条切线长为最左圆左切点到最右圆右切点的距离。4个纸芯有3个间隔，每个间隔为直径3cm，总间隔长=3×3=9cm；加上两边半径（共1个直径），每条切线长=9+3=12cm，两条切线总长=12×2=24cm。
曲线部分：两端半圆合为1个整圆周长，长度=πd=3.14×3=9.42cm（或保留π表示为3π cm）。
总长度=24+3π cm。
小芳的捆法（4个纸芯2×2排列）：
彩绳长度=直线部分+曲线部分。
直线部分：正方形四条边，每条边为相邻两圆外公切线，长=直径3cm，四条边总长=4×3=12cm。
曲线部分：四个角的圆弧合为1个整圆周长，长度=πd=3π cm。
总长度=12+3π cm。
比较：
小明的总长度（24+3π cm）＞小芳的总长度（12+3π cm），两者不相等。
结论：晶晶的说法不正确。