第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第45页
- 第46页
- 第47页
- 第48页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第89页
- 第90页
- 第91页
- 第92页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
17. (每小题4分,共8分)
(1)解方程:$3x^{2}-4x - 5 = 0$.
(2)已知关于$x$的一元二次方程$x^{2}-(2k - 3)x + k^{2}=0$有实数根,求$k$的取值范围.
(1)解方程:$3x^{2}-4x - 5 = 0$.
(2)已知关于$x$的一元二次方程$x^{2}-(2k - 3)x + k^{2}=0$有实数根,求$k$的取值范围.
答案:
17.
(1)解:$a = 3$,$b = - 4$,$c = - 5$.$\Delta = ( - 4 ) ^ { 2 } - 4 × 3 × ( - 5 ) = 76 > 0$.方程有两个不等的实数根$x = \frac { 4 \pm 2 \sqrt { 19 } } { 6 }$,即$x _ { 1 } = \frac { 2 + \sqrt { 19 } } { 3 }$,$x _ { 2 } = \frac { 2 - \sqrt { 19 } } { 3 }$.
(2)解:根据题意,得$\Delta = [ - ( 2 k - 3 ) ] ^ { 2 } - 4 k ^ { 2 } \geqslant 0$.解得$k \leqslant \frac { 3 } { 4 }$.故$k$的取值范围为$k \leqslant \frac { 3 } { 4 }$.
(1)解:$a = 3$,$b = - 4$,$c = - 5$.$\Delta = ( - 4 ) ^ { 2 } - 4 × 3 × ( - 5 ) = 76 > 0$.方程有两个不等的实数根$x = \frac { 4 \pm 2 \sqrt { 19 } } { 6 }$,即$x _ { 1 } = \frac { 2 + \sqrt { 19 } } { 3 }$,$x _ { 2 } = \frac { 2 - \sqrt { 19 } } { 3 }$.
(2)解:根据题意,得$\Delta = [ - ( 2 k - 3 ) ] ^ { 2 } - 4 k ^ { 2 } \geqslant 0$.解得$k \leqslant \frac { 3 } { 4 }$.故$k$的取值范围为$k \leqslant \frac { 3 } { 4 }$.
18. (10分)如图10,在$\triangle ABC$中,$\angle A = 100^{\circ}$,$\angle ABC = 30^{\circ}$,将$\triangle ABC$绕点$B$逆时针旋转$50^{\circ}$后得到$\triangle A_{1}BC_{1}$.求证:$A_{1}C_{1}// BC$.
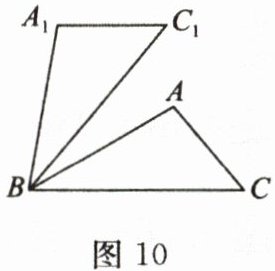

答案:
18.证明:因为$\angle A = 100 ^ { \circ }$,$\angle ABC = 30 ^ { \circ }$,所以$\angle C = 180 ^ { \circ } - \angle A - \angle ABC = 50 ^ { \circ }$.由旋转的性质,得$\angle CBC _ { 1 } = 50 ^ { \circ }$,$\angle C _ { 1 } = \angle C = 50 ^ { \circ }$.所以$\angle CBC _ { 1 } = \angle C _ { 1 }$,所以$A _ { 1 } C _ { 1 } // BC$.
19. (10分)在一个不透明的袋子中有1个黑球和2个白球(除颜色外其他均相同).用画树状图或列表的方法解答下列问题:
(1)小丽第一次从袋子中摸出1个球不放回,第二次又从袋子中摸出1个球.小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出1个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出1个球.小强两次都摸到白球的概率是多少?
(1)小丽第一次从袋子中摸出1个球不放回,第二次又从袋子中摸出1个球.小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出1个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出1个球.小强两次都摸到白球的概率是多少?
答案:
19.解:
(1)画树状图如图31.

由树状图可知,共有6种等可能的结果,两次都摸到白球的结果有2种,所以$P ( 两次都摸到白球 ) = \frac { 2 } { 6 } = \frac { 1 } { 3 }$.
(2)画树状图如图32.

由树状图可知,共有8种等可能的结果,两次都摸到白球的结果有4种,所以$P ( 两次都摸到白球 ) = \frac { 4 } { 8 } = \frac { 1 } { 2 }$.
19.解:
(1)画树状图如图31.

由树状图可知,共有6种等可能的结果,两次都摸到白球的结果有2种,所以$P ( 两次都摸到白球 ) = \frac { 2 } { 6 } = \frac { 1 } { 3 }$.
(2)画树状图如图32.

由树状图可知,共有8种等可能的结果,两次都摸到白球的结果有4种,所以$P ( 两次都摸到白球 ) = \frac { 4 } { 8 } = \frac { 1 } { 2 }$.
20. (10分)如图11,抛物线$y = ax^{2}+bx + c$过点$A(-1,0)$,$B(3,0)$,$M(\frac{3}{2},\frac{15}{4})$,与$y$轴交于点$C$.
(1)求抛物线对应的函数的解析式.
(2)点$P$为抛物线对称轴上的动点,当$\triangle PCB$是以$BC$为底边的等腰三角形时,求点$P$的坐标.
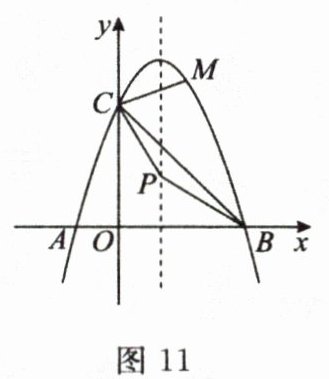
(1)求抛物线对应的函数的解析式.
(2)点$P$为抛物线对称轴上的动点,当$\triangle PCB$是以$BC$为底边的等腰三角形时,求点$P$的坐标.

答案:
20.解:
(1)由抛物线过点$A ( - 1 , 0 )$,$B ( 3 , 0 )$,设抛物线对应的函数的解析式为$y = a ( x + 1 ) ( x - 3 )$.将点$M ( \frac { 3 } { 2 } , \frac { 15 } { 4 } )$代入,得$- \frac { 15 } { 4 } a = \frac { 15 } { 4 }$.解得$a = - 1$.故抛物线对应的函数的解析式为$y = - ( x + 1 ) ( x - 3 )$,即$y = - x ^ { 2 } + 2 x + 3$.
(2)由
(1)可得该抛物线的对称轴为直线$x = - \frac { 2 } { 2 × ( - 1 ) } = 1$.令$x = 0$,得$y = 3$.故点C的坐标为$( 0 , 3 )$.设点P的坐标为$( 1 , m )$.因为$PB = PC$,所以$PB ^ { 2 } = PC ^ { 2 }$,即$( 3 - 1 ) ^ { 2 } + m ^ { 2 } = 1 ^ { 2 } + ( m - 3 ) ^ { 2 }$.解得$m = 1$.所以点P的坐标为$( 1 , 1 )$.
(1)由抛物线过点$A ( - 1 , 0 )$,$B ( 3 , 0 )$,设抛物线对应的函数的解析式为$y = a ( x + 1 ) ( x - 3 )$.将点$M ( \frac { 3 } { 2 } , \frac { 15 } { 4 } )$代入,得$- \frac { 15 } { 4 } a = \frac { 15 } { 4 }$.解得$a = - 1$.故抛物线对应的函数的解析式为$y = - ( x + 1 ) ( x - 3 )$,即$y = - x ^ { 2 } + 2 x + 3$.
(2)由
(1)可得该抛物线的对称轴为直线$x = - \frac { 2 } { 2 × ( - 1 ) } = 1$.令$x = 0$,得$y = 3$.故点C的坐标为$( 0 , 3 )$.设点P的坐标为$( 1 , m )$.因为$PB = PC$,所以$PB ^ { 2 } = PC ^ { 2 }$,即$( 3 - 1 ) ^ { 2 } + m ^ { 2 } = 1 ^ { 2 } + ( m - 3 ) ^ { 2 }$.解得$m = 1$.所以点P的坐标为$( 1 , 1 )$.
21. (10分)如图12,在$\triangle ABC$中,$AB = AC$,以$AC$为直径作$\odot O$交$BC$于点$D$,连接$AD$,过点$D$作$DE\perp AB$,垂足为点$E$,延长$BA$交$\odot O$于点$F$.
(1)求证:$DE$是$\odot O$的切线.
(2)已知$\frac{AE}{DE}=\frac{2}{3}$,$AF = 10$,求$\odot O$的半径.
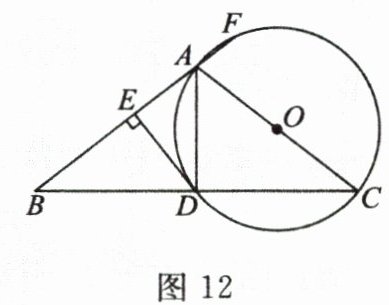
(1)求证:$DE$是$\odot O$的切线.
(2)已知$\frac{AE}{DE}=\frac{2}{3}$,$AF = 10$,求$\odot O$的半径.

答案:
21.
(1)证明:如图33,连接OD.因为$AB = AC$,所以$\angle B = \angle C$.因为$OD = OC$,所以$\angle CDO = \angle C$.所以$\angle CDO = \angle B$,所以$AB // OD$.因为$DE \perp AB$,所以$DE \perp OD$.又OD是$\odot O$的半径,所以$DE$是$\odot O$的切线.
(2)解:如图33,过点O作$OG \perp AF$于点G,则$\angle OGA = 90 ^ { \circ }$,$AG = GF = \frac { 1 } { 2 } AF = 5$.由
(1)知$\angle DEA = \angle ODE = 90 ^ { \circ }$,所以四边形$EDOG$为矩形.所以$OD = EG$,$OG = DE$.由$\frac { AE } { DE } = \frac { 2 } { 3 }$,可设$AE = 2x$,$DE = 3x$.所以$EG = 2x + 5$,$OG = DE = 3x$.所以$OA = OD = EG = 2x + 5$.在$Rt \triangle OAG$中,$OA ^ { 2 } = OG ^ { 2 } + AG ^ { 2 }$,即$( 2 x + 5 ) ^ { 2 } = ( 3 x ) ^ { 2 } + 5 ^ { 2 }$.解得$x _ { 1 } = 4$,$x _ { 2 } = 0$(舍去).所以$OA = 2x + 5 = 13$.故$\odot O$的半径是13.

21.
(1)证明:如图33,连接OD.因为$AB = AC$,所以$\angle B = \angle C$.因为$OD = OC$,所以$\angle CDO = \angle C$.所以$\angle CDO = \angle B$,所以$AB // OD$.因为$DE \perp AB$,所以$DE \perp OD$.又OD是$\odot O$的半径,所以$DE$是$\odot O$的切线.
(2)解:如图33,过点O作$OG \perp AF$于点G,则$\angle OGA = 90 ^ { \circ }$,$AG = GF = \frac { 1 } { 2 } AF = 5$.由
(1)知$\angle DEA = \angle ODE = 90 ^ { \circ }$,所以四边形$EDOG$为矩形.所以$OD = EG$,$OG = DE$.由$\frac { AE } { DE } = \frac { 2 } { 3 }$,可设$AE = 2x$,$DE = 3x$.所以$EG = 2x + 5$,$OG = DE = 3x$.所以$OA = OD = EG = 2x + 5$.在$Rt \triangle OAG$中,$OA ^ { 2 } = OG ^ { 2 } + AG ^ { 2 }$,即$( 2 x + 5 ) ^ { 2 } = ( 3 x ) ^ { 2 } + 5 ^ { 2 }$.解得$x _ { 1 } = 4$,$x _ { 2 } = 0$(舍去).所以$OA = 2x + 5 = 13$.故$\odot O$的半径是13.

22. (12分)综合与实践
【问题情境】
跳台滑雪可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图13中实线部分所示).落地点在着陆坡(如图13中虚线部分所示)上,着陆坡上的基准点$K$为飞行距离计分的参照点,落地点超过点$K$越远,飞行距离分越高.某个跳台滑雪训练场的起跳台的高度$OA$为66m,基准点$K$到起跳台的水平距离为75m,高度为$h$m($h$为定值).设运动员从起跳点$A$起跳后的高度$y$(m)与水平距离$x$(m)之间的函数关系为$y = ax^{2}+bx + c(a\neq0)$.
【初步探究】
(1)$c$的值为
(2)①当运动员落地点恰好为点$K$时,$a = -\frac{1}{50}$,$b = \frac{9}{10}$,求基准点$K$的高度$h$.
②当$a = -\frac{1}{50}$,运动员落地点超过点$K$时,求$b$的取值范围.
【问题情境】
(3)当运动员飞行的水平距离为25m时,恰好达到最大高度76m,试判断他的落地点能否超过点$K$,并说明理由.
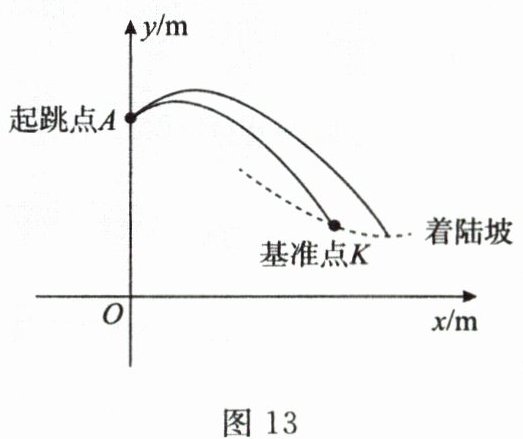
【问题情境】
跳台滑雪可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图13中实线部分所示).落地点在着陆坡(如图13中虚线部分所示)上,着陆坡上的基准点$K$为飞行距离计分的参照点,落地点超过点$K$越远,飞行距离分越高.某个跳台滑雪训练场的起跳台的高度$OA$为66m,基准点$K$到起跳台的水平距离为75m,高度为$h$m($h$为定值).设运动员从起跳点$A$起跳后的高度$y$(m)与水平距离$x$(m)之间的函数关系为$y = ax^{2}+bx + c(a\neq0)$.
【初步探究】
(1)$c$的值为
66
.(2)①当运动员落地点恰好为点$K$时,$a = -\frac{1}{50}$,$b = \frac{9}{10}$,求基准点$K$的高度$h$.
②当$a = -\frac{1}{50}$,运动员落地点超过点$K$时,求$b$的取值范围.
【问题情境】
(3)当运动员飞行的水平距离为25m时,恰好达到最大高度76m,试判断他的落地点能否超过点$K$,并说明理由.

答案:
22.解:
(1)66 提示:把$A ( 0 , 66 )$代入$y = a x ^ { 2 } + b x + c$,得$c = 66$.
(2)①把$a = - \frac { 1 } { 50 }$,$b = \frac { 9 } { 10 }$,$c = 66$代入$y = a x ^ { 2 } + b x + c$,得$y = - \frac { 1 } { 50 } x ^ { 2 } + \frac { 9 } { 10 } x + 66$.把$x = 75$代入$y = - \frac { 1 } { 50 } x ^ { 2 } + \frac { 9 } { 10 } x + 66$,得$y = - \frac { 1 } { 50 } × 75 ^ { 2 } + \frac { 9 } { 10 } × 75 + 66 = 21$.故基准点K的高度$h = 21m$. ②因为$a = - \frac { 1 } { 50 }$,所以$y = - \frac { 1 } { 50 } x ^ { 2 } + b x + 66$.因为运动员落地点超过点K,所以当$x = 75$时,$y > 21$,即$- \frac { 1 } { 50 } × 75 ^ { 2 } + 75 b + 66 > 21$.解得$b > \frac { 9 } { 10 }$.故$b$的取值范围为$b > \frac { 9 } { 10 }$.
(3)他的落地点能超过点K.理由:因为运动员飞行的水平距离为$25m$时,恰好达到最大高度$76m$,所以抛物线的顶点为$( 25 , 76 )$.设抛物线对应的函数解析式为$y = m ( x - 25 ) ^ { 2 } + 76$,把$( 0 , 66 )$代入,得$66 = m ( 0 - 25 ) ^ { 2 } + 76$.解得$m = - \frac { 2 } { 125 }$.所以抛物线对应的函数的解析式为$y = - \frac { 2 } { 125 } ( x - 25 ) ^ { 2 } + 76$.当$x = 75$时,$y = - \frac { 2 } { 125 } × ( 75 - 25 ) ^ { 2 } + 76 = 36$.因为$36 > 21$,所以他的落地点能超过点K.
(1)66 提示:把$A ( 0 , 66 )$代入$y = a x ^ { 2 } + b x + c$,得$c = 66$.
(2)①把$a = - \frac { 1 } { 50 }$,$b = \frac { 9 } { 10 }$,$c = 66$代入$y = a x ^ { 2 } + b x + c$,得$y = - \frac { 1 } { 50 } x ^ { 2 } + \frac { 9 } { 10 } x + 66$.把$x = 75$代入$y = - \frac { 1 } { 50 } x ^ { 2 } + \frac { 9 } { 10 } x + 66$,得$y = - \frac { 1 } { 50 } × 75 ^ { 2 } + \frac { 9 } { 10 } × 75 + 66 = 21$.故基准点K的高度$h = 21m$. ②因为$a = - \frac { 1 } { 50 }$,所以$y = - \frac { 1 } { 50 } x ^ { 2 } + b x + 66$.因为运动员落地点超过点K,所以当$x = 75$时,$y > 21$,即$- \frac { 1 } { 50 } × 75 ^ { 2 } + 75 b + 66 > 21$.解得$b > \frac { 9 } { 10 }$.故$b$的取值范围为$b > \frac { 9 } { 10 }$.
(3)他的落地点能超过点K.理由:因为运动员飞行的水平距离为$25m$时,恰好达到最大高度$76m$,所以抛物线的顶点为$( 25 , 76 )$.设抛物线对应的函数解析式为$y = m ( x - 25 ) ^ { 2 } + 76$,把$( 0 , 66 )$代入,得$66 = m ( 0 - 25 ) ^ { 2 } + 76$.解得$m = - \frac { 2 } { 125 }$.所以抛物线对应的函数的解析式为$y = - \frac { 2 } { 125 } ( x - 25 ) ^ { 2 } + 76$.当$x = 75$时,$y = - \frac { 2 } { 125 } × ( 75 - 25 ) ^ { 2 } + 76 = 36$.因为$36 > 21$,所以他的落地点能超过点K.
查看更多完整答案,请扫码查看


