《2025年新课程学习与测评单元双测九年级数学全一册人教版》

1. 下列方程属于一元二次方程的是(D).

A.$x^{2}+y - 2 = 0$
B.$x + y = 5$
C.$x+\frac{1}{x}=5$
D.$x^{2}+2x = 3$

答案： 1.D

2. 一元二次方程$2x^{2}-3x + 5 = 0$的二次项系数和一次项系数分别是(C).

A.2，5
B.2，3
C.2，$-3$
D.$-3$，2

答案： 2.C

3. 将一元二次方程$x(x - 1) = 2$化为一般形式，结果是(B).

A.$x^{2}-x = 2$
B.$x^{2}-x - 2 = 0$
C.$x^{2}-x + 2 = 0$
D.$x^{2}+x + 2 = 0$

答案： 3.B

4. 用配方法解方程$x^{2}+10x + 9 = 0$，配方后可得(A).

A.$(x + 5)^{2}=16$
B.$(x + 5)^{2}=1$
C.$(x + 10)^{2}=91$
D.$(x + 10)^{2}=109$

答案： 4.A

5. 一元二次方程$x^{2}-x - 3 = 0$的根的情况为(B).

A.有两个相等的实数根
B.有两个不等的实数根
C.只有一个实数根
D.没有实数根

答案： 5.B

6. 已知$m$是方程$2x^{2}-5x - 2 = 0$的一个根，则代数式$2m^{2}-5m$的值是(D).

A.$-2$
B.0
C.1
D.2

答案： 6.D

7. 已知三角形两边的长分别是2和5，第三边的长是方程$x^{2}-7x + 10 = 0$的根，则这个三角形的周长是(A).

A.12
B.9
C.9或12
D.10

答案： 7.A

8. 为执行国家药品降价政策，给人民群众带来实惠，某药品经过两次降价，每盒零售价由16元降为9元.设平均每次降价的百分率是$x$，根据题意列出的方程是(A).

A.$16(1 - x)^{2}=9$
B.$9(1 + x)^{2}=16$
C.$16(1 - 2x)=9$
D.$9(1 + 2x)=16$

答案： 8.A

9. 已知关于$x$的一元二次方程$x^{2}-2kx - k + 1 = 0$的两个实数根分别为$x_{1}$，$x_{2}$，且$x_{1}x_{2}=3$，则$k$的值是(B).

A.2
B.$-2$
C.1
D.$-1$

答案： 9.B 提示：由根与系数的关系，得$x_1x_2=-k + 1$，即$-k + 1 = 3$.解得$k = -2$。

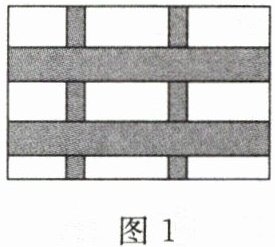
10. 如图1，要设计一幅宽20cm、长30cm的矩形图案，其中有两横两竖的矩形彩条，横、竖彩条的宽度比为$2:1$.要使彩条所占面积是原图案面积的$\frac{19}{75}$，竖彩条的宽度为(A).

A.1cm
B.1.5cm
C.2cm
D.2.5cm

答案： 10.A 提示：设竖彩条的宽度为$x cm$，则横彩条的宽度为$2x cm$.根据题意，得$(30 - 2x)(20 - 4x)=30×20×(1-\frac{19}{75})$，即$x^2 - 20x + 19 = 0$.解得$x_1 = 1$，$x_2 = 19$(不合题意，舍去)。