第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第45页
- 第46页
- 第47页
- 第48页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第89页
- 第90页
- 第91页
- 第92页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
18. (10分)(1)在图6中画出$\triangle ABC$绕点$O$顺时针旋转$90^{\circ}$后得到的$\triangle DEF$.
(2)在图7中画出四边形$ABCD$关于点$O$对称的四边形$A'B'C'D'$.
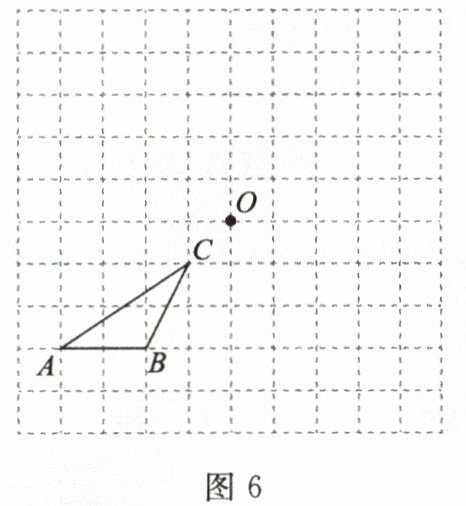
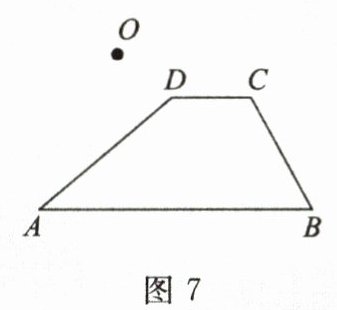
(2)在图7中画出四边形$ABCD$关于点$O$对称的四边形$A'B'C'D'$.


答案:
18.(1)画出△DEF如图9所示;(2)画出四边形A'B'C'D'如图10所示。
19. (10分)已知二次函数$y = x^{2}+4x - 1$.
(1)将二次函数的解析式化为$y = (x + h)^{2}+k$的形式.
(2)写出二次函数图象的开口方向、对称轴和顶点坐标.
(1)将二次函数的解析式化为$y = (x + h)^{2}+k$的形式.
(2)写出二次函数图象的开口方向、对称轴和顶点坐标.
答案:
19.(1)y = (x + 2)² - 5;(2)二次函数的图象开口向上,对称轴为直线x = -2,顶点坐标为(-2, -5)
20. (10分)如图8,将$\triangle ABC$绕点$A$逆时针旋转$45^{\circ}$得到$\triangle ADE$,$\angle BAC = 45^{\circ}$,$AB = 3$,$AC = 4$.
(1)求$\angle EAB$的度数.
(2)连接$BE$,求$BE$的长.
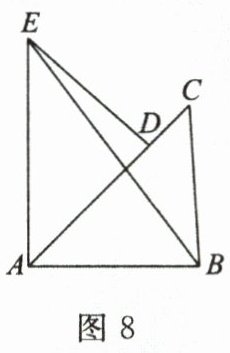
(1)求$\angle EAB$的度数.
(2)连接$BE$,求$BE$的长.

答案:
20.(1)∠EAB = 90°;(2)BE = 5
21. (10分)某超市销售一种商品,每件成本为50元,销售人员调查发现,当该商品的销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,每月可多售出10件,并要求销售单价不得低于每件的成本价且不高于100元,设该商品每月的销售量为$y$(件),销售单价为$x$(元).
(1)求$y$关于$x$的函数解析式.(不要求写出自变量的取值范围)
(2)已知该商品每月的销售利润为4000元,且要使顾客获得更多的实惠,则销售单价应定为多少元?
(3)为了使每月所获利润最大,该商品销售单价应定为多少元?
(1)求$y$关于$x$的函数解析式.(不要求写出自变量的取值范围)
(2)已知该商品每月的销售利润为4000元,且要使顾客获得更多的实惠,则销售单价应定为多少元?
(3)为了使每月所获利润最大,该商品销售单价应定为多少元?
答案:
21.(1)y = -5x + 550;(2)销售单价应定为70元;(3)该商品销售单价应定为80元
22. (12分)综合与实践
【主题】
如何利用闲置硬纸板制作收纳盒,收纳玩具.
【素材】
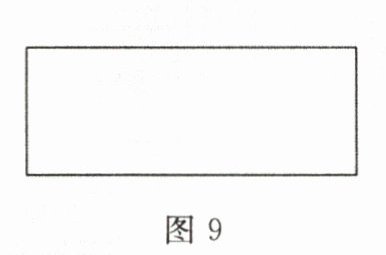
闲置的矩形硬纸板(长为100cm,宽为40cm,如图9).
【目标】
(1)如图10,把矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个长方体无盖收纳盒,该收纳盒的底面积为$1216cm^{2}$,求剪去的小正方形的边长.
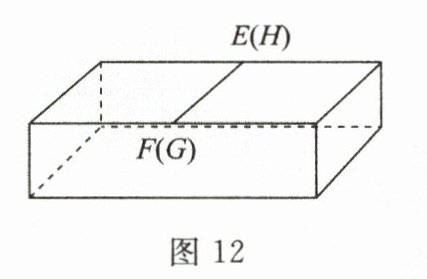
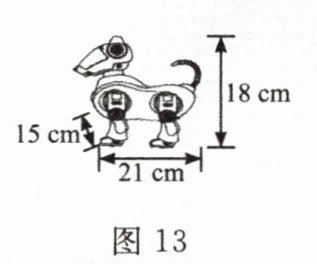
(2)如图11、图12,把矩形硬纸板的四角剪去四个相同的小矩形,使$EF$和$HG$两边恰好重合且无重叠部分,折成一个有盖的长方体收纳盒,盒子的底面积为$702cm^{2}$,小丽家里有一个玩具机械狗,机械狗的实物图和尺寸大小如图13,请通过计算判断玩具机械狗能否完全放入该收纳盒.


【主题】
如何利用闲置硬纸板制作收纳盒,收纳玩具.
【素材】
闲置的矩形硬纸板(长为100cm,宽为40cm,如图9).
【目标】
(1)如图10,把矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个长方体无盖收纳盒,该收纳盒的底面积为$1216cm^{2}$,求剪去的小正方形的边长.
(2)如图11、图12,把矩形硬纸板的四角剪去四个相同的小矩形,使$EF$和$HG$两边恰好重合且无重叠部分,折成一个有盖的长方体收纳盒,盒子的底面积为$702cm^{2}$,小丽家里有一个玩具机械狗,机械狗的实物图和尺寸大小如图13,请通过计算判断玩具机械狗能否完全放入该收纳盒.





答案:
22.(1)剪去的小正方形的边长为12cm;(2)玩具机械狗不能完全放入该收纳盒
查看更多完整答案,请扫码查看


