《2025年新课程学习与测评单元双测九年级数学全一册人教版》

18. 归纳与探究
【问题呈现】
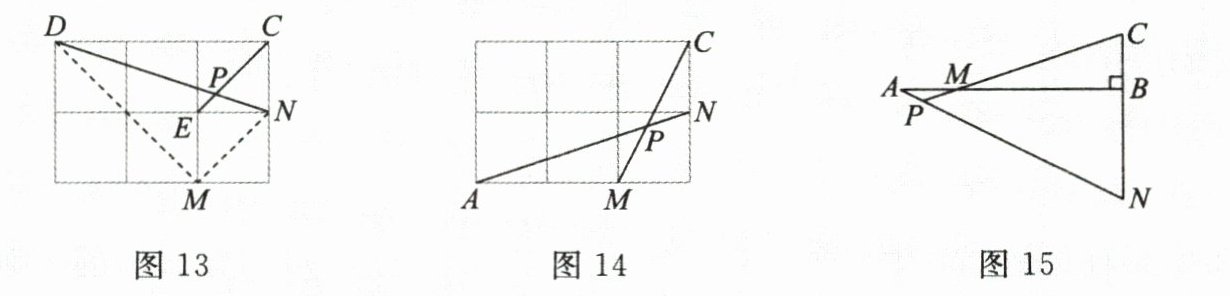
如图13，在边长为1的正方形网格中，分别连接格点D，N和E，C，设DN和EC相交于点P，求tan∠CPN的值.
【方法归纳】
求一个锐角的三角函数值，往往需要找出(或构造出)一个直角三角形.观察发现，问题中∠CPN不在直角三角形中，我们常利用网格画平行线的方法解决此类问题.
示例：如图13，连接格点M，N，可得MN//EC，则∠DNM = ∠CPN.连接DM，∠CPN就转换为Rt△DMN中的∠DNM.
【问题解决】
(1)图13中，tan∠CPN的值为2.
(2)如图14，在边长为1的正方形网格中，AN与CM相交于点P，求cos∠CPN的值.
【思维拓展】
(3)如图15，AB⊥BC，AB = 4BC，点M在AB上，且AM = BC，延长CB到点N，使BN = 2BC，连接AN交CM的延长线于点P.用上述方法构造网格求∠CPN的度数.

答案： 18.
(1)2
(2)如图 43，分别连接格点 A，B 和 B，N，则 AB//CM.所以∠CPN = ∠BAN.由勾股定理，得 AB = BN = $\sqrt{5}$，AN = $\sqrt{10}$.所以 AB² + BN² = AN².所以△ABN 是直角三角形，且∠ABN = 90°.故 cos∠CPN = cos∠BAN = $\frac{AB}{AN}$ = $\frac{\sqrt{5}}{\sqrt{10}}$ = $\frac{\sqrt{2}}{2}$.
(3)设 BC = 1，构造如图 44 所示的网格图，分别连接格点 A，D 和 D，N，则 AD//MC.所以∠CPN = ∠DAN.由勾股定理，得 AD = DN = $\sqrt{10}$，AN = 2$\sqrt{5}$.所以 AD² + DN² = AN².所以△ADN 是直角三角形，且∠ADN = 90°.所以∠DAN = ∠DNA = 45°.故∠CPN = ∠DAN = 45°.