2025年暑假作业贵州人民出版社七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业贵州人民出版社七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
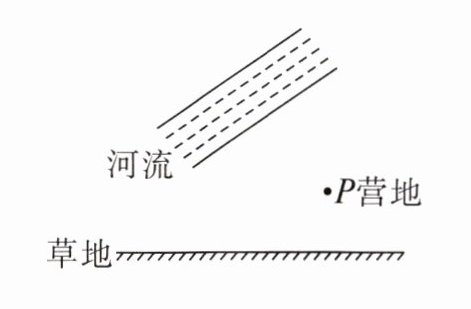
13. 如图,已知牧马营地在 P 处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线。

答案:
解 如图,最短路线为$P→A→B→P$。
最短放牧路线如图所示。

解 如图,最短路线为$P→A→B→P$。
最短放牧路线如图所示。

14. 如图,已知∠AOB,点 M 和点 N 在∠AOB 的内部,试在 OA,OB 上分别找点 P,Q,使四边形 MNQP 的周长最短。(尺规作图,不写作法,保留作图痕迹)


答案:
解 如图,四边形 MNQP 为所求。

解 如图,四边形 MNQP 为所求。

15. 已知点 P 在∠MON 内。如图(1),点 P 关于射线 OM 的对称点是 G,点 P 关于射线 ON 的对称点是 H,连接 OG,OH,OP。
(1)若∠MON = 50°,求∠GOH 的度数;
(2)如图(2),若 OP = 6,当△PAB 的周长最小值为 6 时,求∠MON 的度数。
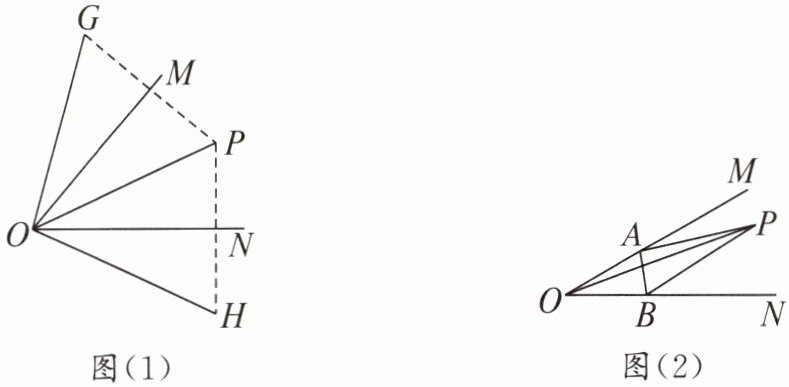
(1)若∠MON = 50°,求∠GOH 的度数;
(2)如图(2),若 OP = 6,当△PAB 的周长最小值为 6 时,求∠MON 的度数。
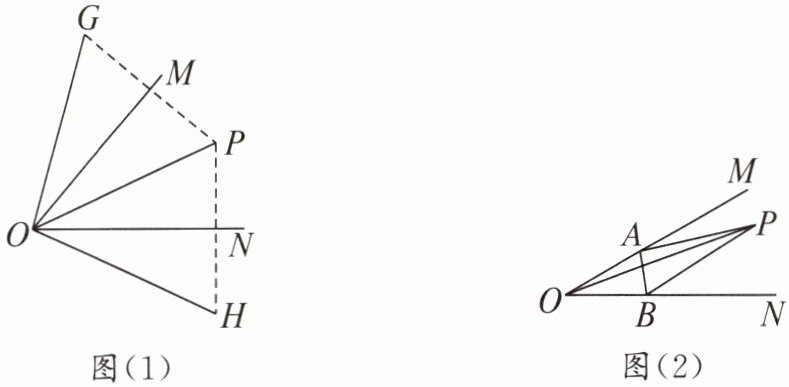
答案:
解
(1)因为点 P 关于射线 OM 的对称点是 G,所以$∠GOM=∠POM$。
因为点 P 关于射线 ON 的对称点是 H,所以$∠HON=∠PON$。
因为$∠MON=∠MOP+∠NOP=50^{\circ }$,所以$∠GOH=∠GOM+∠MOP+∠NOP+∠HON=2∠MON=100^{\circ }$。
(2)如图,作点 P 关于 OM,ON 的对称点$P'$和$P''$,连接$P'P''$,$OP'$,$OP''$。
则$PA=P'A$,$PB=P''B$,$OP'=OP$,$OP''=OP$,$∠P'OM=∠POM$,$∠PON=∠P''ON$。
因为$△PAB$的周长最小值为 6,$OP=6$,所以$P'P''=OP'=OP''=6$,
所以$△OP'P''$为等边三角形,
所以$∠P'OP''=60^{\circ }$。
因为$∠P'OP''=∠P'OM+∠POM+∠PON+∠P''ON=2∠MON$,
所以$∠MON=30^{\circ }$。

解
(1)因为点 P 关于射线 OM 的对称点是 G,所以$∠GOM=∠POM$。
因为点 P 关于射线 ON 的对称点是 H,所以$∠HON=∠PON$。
因为$∠MON=∠MOP+∠NOP=50^{\circ }$,所以$∠GOH=∠GOM+∠MOP+∠NOP+∠HON=2∠MON=100^{\circ }$。
(2)如图,作点 P 关于 OM,ON 的对称点$P'$和$P''$,连接$P'P''$,$OP'$,$OP''$。
则$PA=P'A$,$PB=P''B$,$OP'=OP$,$OP''=OP$,$∠P'OM=∠POM$,$∠PON=∠P''ON$。
因为$△PAB$的周长最小值为 6,$OP=6$,所以$P'P''=OP'=OP''=6$,
所以$△OP'P''$为等边三角形,
所以$∠P'OP''=60^{\circ }$。
因为$∠P'OP''=∠P'OM+∠POM+∠PON+∠P''ON=2∠MON$,
所以$∠MON=30^{\circ }$。

查看更多完整答案,请扫码查看


