《2025年暑假作业贵州人民出版社七年级数学北师大版》

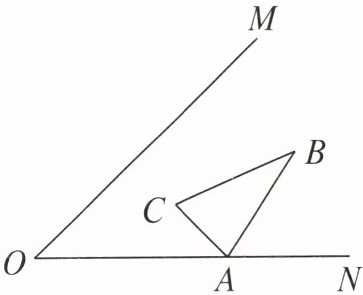
12. 如图,已知$\triangle ABC$,顶点$A在射线ON$上,作出分别以射线$OM,ON为对称轴与\triangle ABC$对称的三角形。

答案：
解 如图。

13. 如图,点$P关于OA和OB轴对称的对称点分别为C,D$,连接$CD$,交$OA于点M$,交$OB于点N$。
(1)若$CD$的长为 18 厘米,求$\triangle PMN$的周长；
(2)若$∠C= 21^{\circ },∠D= 28^{\circ }$,求$∠MPN$的度数。
(1)18 cm
(2)82°

答案： 解
(1)因为点 P 关于 OA 和 OB 的轴对称点分别为 C,D,连接 CD,交 OA 于点 M,交 OB 于点 N,所以$PM=CM,ND=NP$。因为$△PMN$的周长$=PN+PM+MN,PN+PM+MN=CD=18cm,$所以$△PMN$的周长为 18 cm。
(2)因为点 P 关于 OA,OB 的对称点分别是 C,D,所以 OA 垂直平分 PC,OB 垂直平分 PD,所以$CM=PM,PN=DN,$所以$∠C=∠MPC,∠D=∠NPD$。因为$∠PRM=∠PTN=90^{\circ }$,所以在四边形 OTPR 中,$∠CPD+∠O=180^{\circ }$。因为$∠D+∠C+∠CPD=180^{\circ },$所以$∠C+∠D=∠O=49^{\circ },$所以$∠MPN=180^{\circ }-49^{\circ }×2=82^{\circ }$。