《2025年暑假作业贵州人民出版社七年级数学北师大版》

1. 如图,已知 $ AC = BD $,添加下列一个条件后,仍无法判定 $ \triangle ABC \cong \triangle BAD $ 的是(A)
A.$ \angle ABC = \angle BAD $
B.$ \angle C = \angle D = 90 ^ { \circ } $
C.$ \angle CAB = \angle DBA $
D.$ CB = DA $

答案： A

2. 在下列叙述中,两个三角形一定全等的是(D)
A.各有一个角是 $ 45 ^ { \circ } $ 的两个等腰三角形
B.两个等边三角形
C.各有一个角是 $ 45 ^ { \circ } $,腰长都是 $ 3 \mathrm { cm } $ 的两个等腰三角形
D.腰和底角对应相等的两个等腰三角形

答案： D

3. 在 $ \triangle ABC $ 和 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 中,已知 $ \angle A = \angle A ^ { \prime } $,$ \angle B = \angle B ^ { \prime } $,$ AC = A ^ { \prime } C ^ { \prime } $,那么 $ \triangle ABC \cong \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 运用的判定方法是(B)
A.$ SAS $
B.$ AAS $
C.$ ASA $
D.$ SSS $

答案： B

4. 照相机的支架是三条腿,这是利用了三角形的稳定性。现实生活中还有利用三角形的这个特性的例子吗？如果知道,请写出来：自行车的三角梁(写出一个即可)。

答案： 稳定性　自行车的三角梁(答案不唯一)

5. 如图,要判定 $ \triangle ACF \cong \triangle BDE $,根据给定的条件和指明的依据,将应当添加的条件填在横线上。

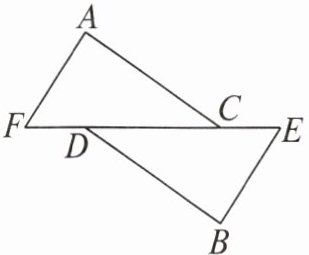
(1)若 $ AC // BD $,$ AC = BD $,____∠A = ∠B____,则 $ \triangle ACF \cong \triangle BDE ( ASA ) $；
(2)若 $ AC // BD $,____∠F = ∠E(或AF // EB)____,$ AC = BD $,则 $ \triangle ACF \cong \triangle BDE ( AAS ) $。

答案：
(1)∠A = ∠B
(2)∠F = ∠E(或AF // EB)

6. 如图,已知 $ AD = AE $,$ BD = CE $,$ AF \perp BC $ 于点 $ F $,且 $ F $ 是 $ BC $ 的中点,试说明 $ \angle D = \angle E $。

答案：
解：如图，连接AB，AC，因为F是BC的中点，
所以BF = CF。
因为AF⊥BC，
所以∠AFB = ∠AFC = 90°。
在△ABF和△ACF中，
因为BF = CF，∠AFB = ∠AFC，AF = AF，根据三角形全等的判定条件“SAS”，所以△ABF≌△ACF，
所以AB = AC。
在△ABD和△ACE中，因为AD = AE，BD = CE，AB = AC，
根据三角形全等的判定条件“SSS”，所以△ABD≌△ACE，
所以∠D = ∠E。