《2025年暑假作业贵州人民出版社七年级数学北师大版》

8. 一个三角形两边长分别为$3$,$7$,若它的周长是小于$16$的整数,则第三边的长为(C)
A.$1$
B.$3$
C.$5$
D.$7$

答案： C

9. 如图,$A$,$B$,$C分别是线段A_{1}B$,$B_{1}C$,$C_{1}A$的中点,若$\triangle ABC的面积是1$,则$\triangle A_{1}B_{1}C_{1}$的面积是(D)
A.$4$
B.$5$
C.$6$
D.$7$

答案： D

10. 在三角形中,如果有一个内角是另外一个内角的$2$倍,我们把这个三角形叫做“二倍角三角形”。在一个“二倍角三角形”中,有一个内角为$30^{\circ}$,则另外两个内角的度数分别为$100^{\circ}, 50^{\circ}$ 或 $90^{\circ}, 60^{\circ}$ 或 $135^{\circ}, 15^{\circ}$。

答案： $100^{\circ}, 50^{\circ}$ 或 $90^{\circ}, 60^{\circ}$ 或 $135^{\circ}, 15^{\circ}$

11. 已知等腰三角形的周长是$16\mathrm{cm}$。
(1)若其中一边的长为$4\mathrm{cm}$,求另外两边的长；
(2)若其中一边的长为$6\mathrm{cm}$,求另外两边的长。

答案： 解
(1) 若腰长为 4 cm，则底边长为 $16 - 4 - 4 = 8(cm)$。
三边长分别为 4 cm，4 cm，8 cm，不符合三角形三边关系，所以应该是底边长为 4 cm，则腰长为 $(16 - 4) ÷ 2 = (16 - 4) ÷ 2 = 6(cm)$。
三边长分别为 4 cm，6 cm，6 cm，符合三角形三边关系。
所以另外两边的长都为 6 cm。
(2) 若腰长为 6 cm，则底边长为 $16 - 6 - 6 = 4(cm)$。
三边长分别为 4 cm，6 cm，6 cm，符合三角形三边关系。
此时另外两边的长分别为 6 cm 和 4 cm。
若底边长为 6 cm，则腰长为 $(16 - 6) ÷ 2 = 5(cm)$。
三边长分别为 6 cm，5 cm，5 cm，符合三角形三边关系。
此时另外两边的长都为 5 cm。
综上可知，另外两边的长为 6 cm，4 cm 或均为 5 cm。

12. 如图,已知$\triangle ABC$为钝角三角形。
(1)作出$\triangle ABC的高AM$,$CN$；
(2)若$CN = 3$,$AM = 6$,求边$BC与AB$的比值。

答案：
解
(1)如图，AM CN 即为所求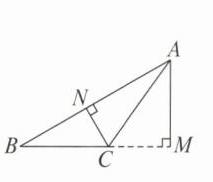
( ) 因为 AM，CN 均为 $\triangle ABC$ 的高，
所以 $\triangle ABC$ 的面积 $S_{\triangle ABC}= \frac{1}{2}AM \cdot BC = \frac{1}{2}CN \cdot AB$，所以 $AM \cdot BC = CN \cdot AB$。又 $CN = 3$，$AM = 6$，所以 $6BC = 3AB$，
所以 $\frac{BC}{AB} = \frac{1}{2}$。