《2025年暑假作业贵州人民出版社七年级数学北师大版》

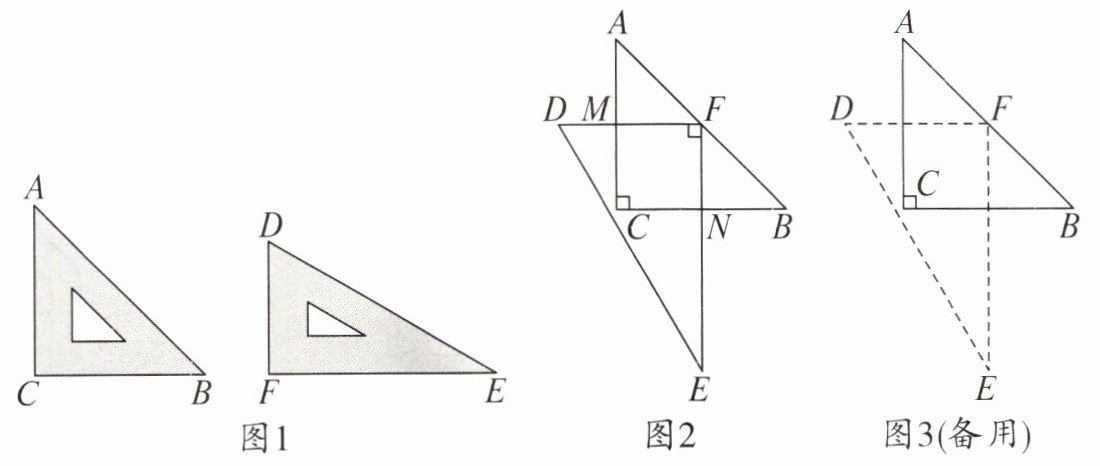
15. 三角板是我们数学学习必不可少的工具,如图 1 是一副含 $ 45 ^ { \circ } $ 和 $ 30 ^ { \circ } $ 角的三角板,其中在三角形 $ ABC $ 中, $ \angle A = \angle B = 45 ^ { \circ } $, $ AC = BC $;在三角形 $ DEF $ 中, $ \angle D = 60 ^ { \circ } $, $ \angle E = 30 ^ { \circ } $。现在我们进行如下操作:把含 $ 30 ^ { \circ } $ 角的三角板的直角顶点 $ F $ 位于另一三角板的斜边中点上,边 $ FD $ 与 $ AC $ 相交于点 $ M $,边 $ FE $ 与 $ BC $ 相交于点 $ N $,将三角板 $ DEF $ 绕点 $ F $ 旋转,点 $ M $, $ N $ 分别在线段 $ AC $, $ BC $ 上相应移动。
(1)请你探究:当 $ \angle AFD = 45 ^ { \circ } $ 时(如图 2), $ FM $ 与 $ FN $ 有怎样的数量关系? 请说明理由。
(2)请你猜想:在三角板 $ DEF $ 绕点 $ F $ 旋转过程中,(1)中 $ FM $ 与 $ FN $ 的数量关系还成立吗?如果成立,请说明理由;如果不成立,请举例说明(图 3 供实验操作备用)。

答案：
解
(1)因为F为AB的中点，所以AF = BF。
因为∠AFM = 45°，∠DFE = 90°，所以∠BFN = 180° - ∠AFM - ∠DFE = 180° - 45° - 90° = 45°。
所以∠AFM = ∠BFN。
在△AFM和△FBN中，因为∠B = ∠A，AF = BF，∠AFM = ∠BFN，根据三角形全等的判定条件“ASA”，所以△AFM ≌ △BFN。所以FM = FN。
(2)猜想：FM = FN仍然成立。理由如下：
如图，

因为∠M₀FN₀ = ∠MFN = 90°，所以∠M₀FN₀ - ∠MFN₀ = ∠MFN - ∠MFN₀，即∠M₀FM = ∠N₀FN。
因为∠MM₀F为△AM₀F的外角，所以∠MM₀F = ∠A + ∠AFM₀ = 2 × 45° = 90°。
因为∠FN₀B = 180° - ∠B - ∠BFN₀ = 90°，所以∠MM₀F = ∠NN₀F。
又由
(1)可知，M₀F = N₀F。
在△MM₀F和△NN₀F中，∠M₀FM = ∠N₀FN，M₀F = N₀F，∠MM₀F = ∠NN₀F，根据三角形全等的判定条件“ASA”，所以△MM₀F ≌ △NN₀F。所以FM = FN。