第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
一、递等式计算,能简算的要简算。
$15.68-(7.78-4.32)-2.32$
$1000÷(0.125+1.25+0.025+0.2)$
$0.25×(0.875×2+0.875×2)$
$15.68-(7.78-4.32)-2.32$
$1000÷(0.125+1.25+0.025+0.2)$
$0.25×(0.875×2+0.875×2)$
答案:
15.68-(7.78-4.32)-2.32=15.68-7.78+4.32-2.32=(15.68+4.32)-(7.78+2.32)=20-10.1=9.9 1000÷(0.125+1.25+0.025+0.2)=1000÷1.6=625 0.25×(0.875×2+0.875×2)=0.25×0.875×4=0.25×4×0.875=1×0.875=0.875
1. 三个连续自然数,若最小的数是$m$,则这三个数的和是
3m+3
;若三个连续自然数的和是$n$,则最小的自然数是n÷3-1
。
答案:
3m+3 n÷3-1
2. 一本书一共有$a$页。冬冬每天看15页,6天后还剩
a-90
页;当$a$是165
时,照这样的速度再看5天就能全部看完。
答案:
a-90 165
3. 从4根4厘米、4根2厘米和4根1厘米长的小棒中,选出若干根,使它们首尾相接,能够摆出(
7
)种大小不同的正方形。
答案:
7
六年级5个班进行足球比赛,每两个班之间都踢一场。到现在为止,一班踢了2场,二班踢了4场,三班踢了4场,四班踢了3场,那么五班已经踢了(
3
)场比赛。
答案:
3
5. 用4种不同的颜色对下图中四个部分进行涂色,相邻两块不能用同一种颜色,则共有(
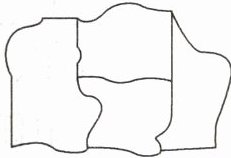
48
)种不同的涂色方法。
答案:
48 提示:先给最左边那块涂色,有 4种选择,再给中间上面那块涂色,有 3种选择,中间下面那块只有 2种选择,最右边那块与中间 2块相邻,也只有 2种颜色选择,根据乘法原理:4×3×2×2=48(种)。
1. 4个好朋友去公园玩,照相时,必须有一个人给其他三个人拍照(三人站一排)。一共有多少种拍照情况?
答案:
4×3×2×1=24(种) 提示:4名同学选一名拍照有 4种选法,剩下的 3人站一排,最左边有 3种选法,中间只有 2种选法,最右边只有 1种选法。
2. 公园里有一个长$a$米、宽$b$米的广场(如右图)。扩建时,长和宽各增加了30米。
(1) 用含有字母的式子表示扩建后广场的面积。
(2) 当$a= 150$,$b= 120$时,扩建时广场面积增加多少平方米?
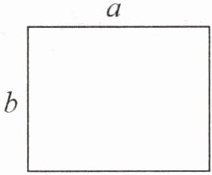
(1) 用含有字母的式子表示扩建后广场的面积。
(a+30)(b+30)
(2) 当$a= 150$,$b= 120$时,扩建时广场面积增加多少平方米?
9000

答案:
(1)(a+30)(b+30)
(2)增加的面积:(a+30)(b+30)-ab 当 a=150,b=120 时,(a+30)(b+30)-ab=(150+30)×(120+30)-150×120=9000。
(1)(a+30)(b+30)
(2)增加的面积:(a+30)(b+30)-ab 当 a=150,b=120 时,(a+30)(b+30)-ab=(150+30)×(120+30)-150×120=9000。
3. 下图是某月的月历卡,用 去框月历卡里的日期数,每次框出5个数。
去框月历卡里的日期数,每次框出5个数。
(1) 若用$m$表示中间的那个数,则每次框出的五个数的和可以表示为(
(2) 共可以框出(
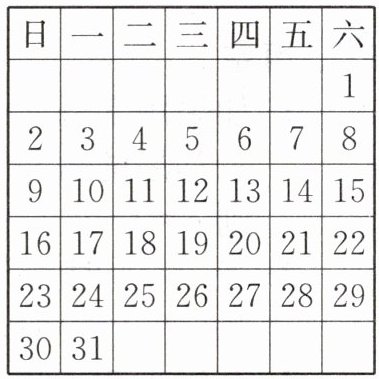
 去框月历卡里的日期数,每次框出5个数。
去框月历卡里的日期数,每次框出5个数。(1) 若用$m$表示中间的那个数,则每次框出的五个数的和可以表示为(
5m
)。(2) 共可以框出(
10
)个不同的和,其中和最大是(105
)。
答案:
(1)5m
(2)10 105
(1)5m
(2)10 105
4. 如图是一个六边形的点阵,它的中心是1个点,算作第一层,第二层每边2个点,第三层每边3个点……以此类推。
(1) 填写下表。
|层数|1|2|3|4|5|…|$n(n≥2)$|
|此层点数|1|6|12|
(2) 当$n= 15$时,该层一共有多少个点?
(1) 填写下表。
|层数|1|2|3|4|5|…|$n(n≥2)$|
|此层点数|1|6|12|
18
|24
|…|6n-6
|(2) 当$n= 15$时,该层一共有多少个点?
当 n=15 时,6n-6=6×15-6=84
答案:
(1)见下表
层数
1
2
3
4
5
…
n(n≥2)
此层点数
1
6
12
18
24
…
6n-6
(2)当 n=15 时,6n-6=6×15-6=84
(1)见下表
层数
1
2
3
4
5
…
n(n≥2)
此层点数
1
6
12
18
24
…
6n-6
(2)当 n=15 时,6n-6=6×15-6=84
查看更多完整答案,请扫码查看


