《2025年从课本到奥数五年级数学上册苏教版》

(1) 一个直角梯形的周长是64分米,它的两条腰长分别是13分米、15分米,这个直角梯形的面积是(234)平方分米。

答案： 234

(2) 用两个完全一样的直角梯形一定能拼成一个长方形,如果长方形的长是12厘米,宽是8厘米,每个梯形的面积是(48)平方厘米。如果每个梯形的面积是30平方厘米,那么拼成的长方形的面积是(60)平方厘米。

答案： 48　60

(3) 如图,一个梯形被分成一个平行四边形和一个三角形。若梯形面积是30平方厘米,则三角形面积是(10)平方厘米。

答案： 10

2. 一批木材堆成梯形形状。最底层有8根,每相邻两层相差1根,最上层有2根。这堆木材一共有多少根?

答案： (2+8)×(8−2+1)÷2=35(根)　提示:分析题意可知上底为2，下底为8，每相邻两层相差1根，则高为8−2+1=7，根据梯形的面积公式即可求得。

3. 一块直角梯形的菜地,它的下底是30米,如果上底增加18米,这块地就变成了正方形。这块梯形菜地的面积是多少平方米?

答案： 30−18=12(米)　(12+30)×30÷2=630(平方米)　提示:根据题意可得，梯形的高是30米，上底为30−18=12(米)。

4. 如图,阴影部分的面积是6平方厘米,求梯形的面积。

答案： 6×2÷3=4(厘米)　(3+5)×4÷2=16(平方厘米)　提示:分析题意可求得三角形的高，三角形的高就是梯形的高。再根据梯形的面积公式即可求得梯形的面积。

例 连接一个梯形的两条对角线相交于点O,把梯形分成了4个三角形(如下图)。

(1) 甲面积与乙面积相比,哪个大?
(2) 若甲面积是8平方厘米,丙面积是4平方厘米,则梯形的面积是多少平方厘米?
分析与解答 (1) 三角形ACD与三角形BCD等底等高,面积相等,即甲面积+丁面积= 乙面积+丁面积,两边去掉相同的丁面积,得甲面积= 乙面积。
(2) 甲、丙两个三角形若以A为顶点,则高相同,甲面积却是丙面积的2倍,所以CO= 2BO;乙与丁两个三角形若以D为顶点,则高相同,而丁的底是乙的底的2倍,所以丁面积是乙面积的2倍。
(1) 甲面积与乙面积相等。
(2) 丁面积:$8×2= 16$(平方厘米)
梯形面积:$4+8+8+16= 36$(平方厘米)
小窍门 在梯形中借助等底等高的三角形面积相等来解决相关问题,同时关注不同三角形间,由于底与高之间的倍数关系导致的面积间的倍数关系。

答案： 解析：
(1) 题目考查梯形中三角形的面积比较。通过观察可以发现，三角形ACD与三角形BCD等底等高，所以面积相等。通过等量代换，可以得到甲和乙的面积相等。
(2) 题目考查梯形中三角形面积与梯形面积的关系。已知甲面积是丙面积的2倍，可以得出甲和丙的高相同，底边有倍数关系。同理，乙和丁的面积也有相应的倍数关系。通过计算可以得到梯形的总面积。
答案：
(1) 甲面积与乙面积相等。
(2) 梯形的面积是36平方厘米。

1. 如图,梯形中有几对面积相等的三角形?

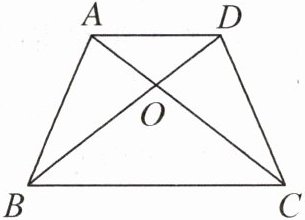
答案： 3对　分别是三角形ABC和三角形BCD，三角形ABO和三角形DOC，三角形ABD和三角形ADC

2. 如图,梯形的对角线把梯形分成4个小三角形,其中两个小三角形的面积为6平方厘米和18平方厘米,则梯形的面积是多少平方厘米?

答案：
6+6+18+2=32(平方厘米)　提示:如图，面积为18的三角形
　　　　　　　　　　　　　　 是面积为6的三角形面积的3倍，因为高相同，所以底的关系也是3倍关系，甲与乙等高，所以甲面积是乙面积的3倍，且甲的面积为6，则乙面积为6÷3=2(平方厘米)，以此求出梯形的面积。