《2025年从课本到奥数五年级数学上册苏教版》

1. 计算下面阴影部分的面积。
(1)

(2)

(3)

答案：
(1)(10 - 6)×6÷2 = 12(平方厘米) 提示:充分利用45°角得到有用的条件。
(2)8×4÷2 = 16(平方厘米)
(3)6×6 + 4×4 - 6×(6 + 4)÷2 = 22(平方厘米)

2. 把一个组合图形分成三块,分别用A、B、C表示,A的面积比B的面积大多少平方厘米？(单位:厘米)

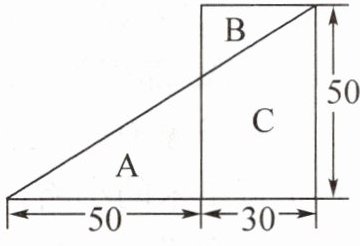
答案： 50×(50 + 30)÷2 = 2000(平方厘米) 30×50 = 1500(平方厘米) 2000 - 1500 = 500(平方厘米) 提示:A和B分别加上C，就得到一个大三角形和一个长方形，用大三角形的面积减去长方形的面积就是A比B大的面积。

3. 下图是一块长方形广场绿地,绿地长24米,宽16米,中间有一条宽2米的道路,求绿地(阴影部分)的面积。

答案： (24 - 2)×(16 - 2)=308(平方米)

4. 一张长方形红纸,长120厘米,宽80厘米,要剪出底和高都是20厘米的等腰直角三角形做成小旗,最多可以做多少面小旗?

答案： 120÷20×(80÷20)×2 = 48(个) 提示:每个边长20厘米的正方形都可以剪成2个符合条件的三角形。

例 已知大正方形ABFG的边长是6厘米,小正方形BCDE的边长是4厘米,求阴影部分的面积。

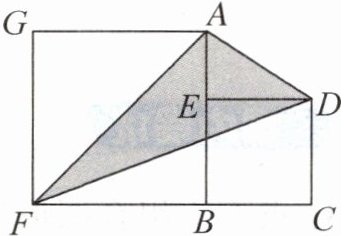
分析与解答 阴影部分的面积可看成是大正方形的面积和梯形ABCD的面积之和,再剔除空白部分两个三角形的面积。
大正方形的面积：$6×6= 36$(平方厘米)
梯形ABCD的面积：$(4+6)×4÷2= 20$(平方厘米)
空白部分两个三角形的面积：
$6×6÷2= 18$(平方厘米)
$(4+6)×4÷2= 20$(平方厘米)
阴影部分的面积：
$36+20-18-20= 18$(平方厘米)
小窍门 先整体观察图形,看它是由哪几个图形组成的,空白部分的面积如果能求出来,就可以用整体面积剔除空白部分的面积。

答案： 大正方形ABFG的面积：6×6=36(平方厘米)
梯形ABCD的面积：(4+6)×4÷2=20(平方厘米)
三角形AFG的面积：6×6÷2=18(平方厘米)
三角形FCD的面积：(4+6)×4÷2=20(平方厘米)
阴影部分的面积：36+20-18-20=18(平方厘米)
答：阴影部分的面积是18平方厘米。

1. 已知平行四边形的面积是128平方厘米,E、F分别是两边上的中点。求阴影部分的面积。

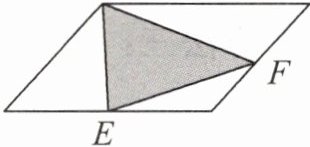
答案：
128÷4×2 + 128÷8 = 80(平方厘米) 128 - 80 = 48(平方厘米) 提示:如图，甲、乙面积是平行四边形面积的四分之一，即128÷4，丙面积是平行四边形面积的八分之一，即128÷8。

2. 在直角梯形ABCD中,$AE= ED,BC= 18$厘米,$BC= 3FC,AD= 6$厘米,$CD= 6$厘米,且三角形EGD的面积与三角形CGF的面积相等。求阴影部分的面积。

答案： AE = DE = 6÷2 = 3(厘米) CF = 18÷3 = 6(厘米) CG = 6÷(2 + 1)=2(厘米) 三角形CGF的面积:6×2÷2 = 6(平方厘米) 所有空白部分的面积:6×(2 + 3)=30(平方厘米) 阴影部分的面积:(6 + 18)×6÷2 - 30 = 42(平方厘米) 提示:FC = 18÷3 = 6(厘米),BF = 18 - 6 = 12(厘米)，三角形BFG的面积是三角形CFG的2倍。AE = ED = 3厘米,三角形AEG、三角形EGD与三角形CFG的面积相等。因为FC = 2ED，所以DG = 2CG，所以CG = 6÷(2 + 1)=2(厘米)。