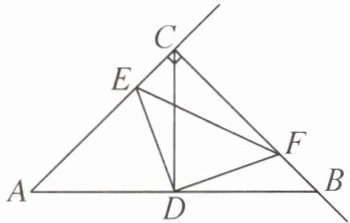
例12 (扬州市邗江区期中)如图,在等腰直角三角形$ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC = 6$,$D是AB$的中点,点$E$,$F分别在射线AC与射线CB$上运动,且满足$AE = CF$,则在运动过程中,$\triangle DEF$面积的最小值为______
$\frac{9}{2}$
.
答案:
解:过点$D$分别作$DH\perp AC$于点$H$,$DG\perp BC$于点$G$。
在等腰直角三角形$ABC$中,$\angle ACB=90^{\circ}$,$AC=BC=6$,$D$是$AB$中点,
$\therefore CD=AD=BD$,$\angle ACD=\angle BCD=45^{\circ}$,$DH=DG=3$($DH$为$AC$边上中线的一半,即$\frac{1}{2}AC=3$)。
$\because AE=CF$,$AC=BC$,$\therefore CE=BF$。
在$\triangle CED$和$\triangle BFD$中,
$\left\{\begin{array}{l}CE=BF\\\angle ECD=\angle FBD=45^{\circ}\\CD=BD\end{array}\right.$,
$\therefore\triangle CED\cong\triangle BFD(SAS)$,$\therefore ED=FD$,$\angle EDC=\angle FDB$。
$\because\angle CDB=90^{\circ}$,$\therefore\angle EDF=\angle EDC+\angle CDF=\angle FDB+\angle CDF=\angle CDB=90^{\circ}$,
$\therefore\triangle EDF$是等腰直角三角形,$S_{\triangle DEF}=\frac{1}{2}ED^{2}$。
当$ED\perp AC$时,$ED$最小,此时$ED=DH=3$,
$\therefore S_{\triangle DEF}$最小值为$\frac{1}{2}×3^{2}=\frac{9}{2}$。
答案:$\frac{9}{2}$
在等腰直角三角形$ABC$中,$\angle ACB=90^{\circ}$,$AC=BC=6$,$D$是$AB$中点,
$\therefore CD=AD=BD$,$\angle ACD=\angle BCD=45^{\circ}$,$DH=DG=3$($DH$为$AC$边上中线的一半,即$\frac{1}{2}AC=3$)。
$\because AE=CF$,$AC=BC$,$\therefore CE=BF$。
在$\triangle CED$和$\triangle BFD$中,
$\left\{\begin{array}{l}CE=BF\\\angle ECD=\angle FBD=45^{\circ}\\CD=BD\end{array}\right.$,
$\therefore\triangle CED\cong\triangle BFD(SAS)$,$\therefore ED=FD$,$\angle EDC=\angle FDB$。
$\because\angle CDB=90^{\circ}$,$\therefore\angle EDF=\angle EDC+\angle CDF=\angle FDB+\angle CDF=\angle CDB=90^{\circ}$,
$\therefore\triangle EDF$是等腰直角三角形,$S_{\triangle DEF}=\frac{1}{2}ED^{2}$。
当$ED\perp AC$时,$ED$最小,此时$ED=DH=3$,
$\therefore S_{\triangle DEF}$最小值为$\frac{1}{2}×3^{2}=\frac{9}{2}$。
答案:$\frac{9}{2}$
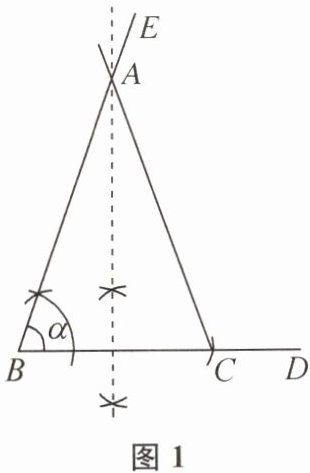
例13 (南京市玄武区期末)如图,已知$\angle\alpha和线段a$.用无刻度的直尺和圆规按下列要求作图(保留作图痕迹,写出必要的文字说明).
(1)作出一个等腰三角形$ABC$,使其底角为$\alpha$,底边长为$a$;
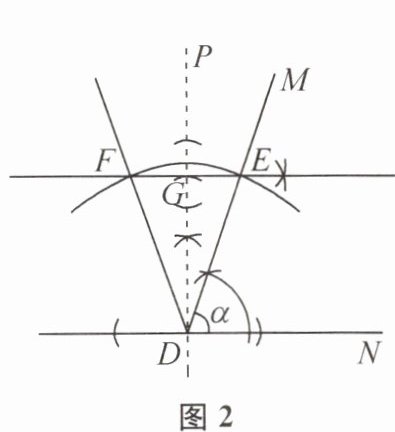
(2)作出一个等腰三角形$DEF$,使其底角为$\alpha$,底边上的高为$a$.
分析 (1)根据条件,依据“ASA”,可确定$\triangle ABC$.可先作底边$BC = a$,然后作底角$\angle ABC = \angle ACB = \alpha$,从而确定顶点$A$;当然也可以在确定底边$BC和底角\angle ABC$后,利用等腰三角形的轴对称性确定点$A$.(2)根据条件,已知等腰三角形的底角和底边上的高,依据“AAS”,由这两个条件确定的三角形是可以作出来的,但要转化成“ASA”,即先构造出$\angle\alpha$的余角.

答案 (1)如图1,作$\angle EBD = \alpha$,在射线$BD上截取BC = a$.作$BC$的垂直平分线,交射线$BE于点A$,连接$AC$.则$\triangle ABC$即为所作.
(2)答案不唯一,以下作法供参考.
作法一:如图2,作$\angle MDN = \alpha$,过点$D作DP\perp DN$,在射线$DP上截取DG = a$.过点$G作GE\perp DG$,交射线$DM于点E$.以点$D$为圆心,$DE$的长为半径画弧,交直线$GE于点F$,连接$DF$.则$\triangle DEF$即为所作.
作法二:如图3,作直线$MN$,在直线$MN上任取一点O$,过点$O作直线MN的垂线l$,在直线$l上截取OD = a$.作$\angle MOP = \alpha$,作$OD$的垂直平分线,交射线$OP于点Q$,连接$DQ并延长交直线MN于点E$.以点$D$为圆心,$DE$的长为半径画弧,交直线$MN于点F$,连接$DF$.则$\triangle DEF$即为所作.
作法三:如图4,作直线$l_{1}$,在直线$l_{1}上任取一点O$,过点$O作直线l_{1}的垂线l_{2}$,在垂线$l_{2}上截取OD = a$.作$\angle\alpha的余角\angle\beta$,作$\angle ODE = \beta$,交直线$l_{1}于点E$.以点$D$为圆心,$DE$长为半径画弧,交直线$l_{1}于点F$,连接$DF$.则$\triangle DEF$即为所作.
(1)作出一个等腰三角形$ABC$,使其底角为$\alpha$,底边长为$a$;
(2)作出一个等腰三角形$DEF$,使其底角为$\alpha$,底边上的高为$a$.
分析 (1)根据条件,依据“ASA”,可确定$\triangle ABC$.可先作底边$BC = a$,然后作底角$\angle ABC = \angle ACB = \alpha$,从而确定顶点$A$;当然也可以在确定底边$BC和底角\angle ABC$后,利用等腰三角形的轴对称性确定点$A$.(2)根据条件,已知等腰三角形的底角和底边上的高,依据“AAS”,由这两个条件确定的三角形是可以作出来的,但要转化成“ASA”,即先构造出$\angle\alpha$的余角.

答案 (1)如图1,作$\angle EBD = \alpha$,在射线$BD上截取BC = a$.作$BC$的垂直平分线,交射线$BE于点A$,连接$AC$.则$\triangle ABC$即为所作.
(2)答案不唯一,以下作法供参考.
作法一:如图2,作$\angle MDN = \alpha$,过点$D作DP\perp DN$,在射线$DP上截取DG = a$.过点$G作GE\perp DG$,交射线$DM于点E$.以点$D$为圆心,$DE$的长为半径画弧,交直线$GE于点F$,连接$DF$.则$\triangle DEF$即为所作.
作法二:如图3,作直线$MN$,在直线$MN上任取一点O$,过点$O作直线MN的垂线l$,在直线$l上截取OD = a$.作$\angle MOP = \alpha$,作$OD$的垂直平分线,交射线$OP于点Q$,连接$DQ并延长交直线MN于点E$.以点$D$为圆心,$DE$的长为半径画弧,交直线$MN于点F$,连接$DF$.则$\triangle DEF$即为所作.
作法三:如图4,作直线$l_{1}$,在直线$l_{1}上任取一点O$,过点$O作直线l_{1}的垂线l_{2}$,在垂线$l_{2}上截取OD = a$.作$\angle\alpha的余角\angle\beta$,作$\angle ODE = \beta$,交直线$l_{1}于点E$.以点$D$为圆心,$DE$长为半径画弧,交直线$l_{1}于点F$,连接$DF$.则$\triangle DEF$即为所作.


答案:
【解析】:
本题主要考查等腰三角形的性质和尺规作图。
(1)已知底边长和底角,根据“ASA”来确定等腰三角形。先作出底边,再以底边的两个端点为顶点,作出底角,两个底角的另一边相交于一点,该点即为等腰三角形的顶点。
(2)已知底角和底边上的高,可先构造出底角的余角,再利用“AAS”来确定三角形,或者通过其他几何关系,如点到直线的距离等知识来作出满足条件的等腰三角形。
【答案】:
(1)如图1,作$\angle EBD = \alpha$,在射线$BD$上截取$BC = a$。作$BC$的垂直平分线,交射线$BE$于点$A$,连接$AC$。则$\triangle ABC$即为所作。
(2)答案不唯一,以下作法供参考。
作法一:如图2,作$\angle MDN = \alpha$,过点$D$作$DP \perp DN$,在射线$DP$上截取$DG = a$。过点$G$作$GE \perp DG$,交射线$DM$于点$E$。以点$D$为圆心,$DE$的长为半径画弧,交直线$GE$于点$F$,连接$DF$。则$\triangle DEF$即为所作。
作法二:如图3,作直线$MN$,在直线$MN$上任取一点$O$,过点$O$作直线$MN$的垂线$l$,在直线$l$上截取$OD = a$。作$\angle MOP = \alpha$,作$OD$的垂直平分线,交射线$OP$于点$Q$,连接$DQ$并延长交直线$MN$于点$E$。以点$D$为圆心,$DE$的长为半径画弧,交直线$MN$于点$F$,连接$DF$。则$\triangle DEF$即为所作。
作法三:如图4,作直线$l_1$,在直线$l_1$上任取一点$O$,过点$O$作直线$l_1$的垂线$l_2$,在垂线$l_2$上截取$OD = a$。作$\angle \alpha$的余角$\angle \beta$,作$\angle ODE = \beta$,交直线$l_1$于点$E$。以点$D$为圆心,$DE$长为半径画弧,交直线$l_1$于点$F$,连接$DF$。则$\triangle DEF$即为所作。
图略。
本题主要考查等腰三角形的性质和尺规作图。
(1)已知底边长和底角,根据“ASA”来确定等腰三角形。先作出底边,再以底边的两个端点为顶点,作出底角,两个底角的另一边相交于一点,该点即为等腰三角形的顶点。
(2)已知底角和底边上的高,可先构造出底角的余角,再利用“AAS”来确定三角形,或者通过其他几何关系,如点到直线的距离等知识来作出满足条件的等腰三角形。
【答案】:
(1)如图1,作$\angle EBD = \alpha$,在射线$BD$上截取$BC = a$。作$BC$的垂直平分线,交射线$BE$于点$A$,连接$AC$。则$\triangle ABC$即为所作。
(2)答案不唯一,以下作法供参考。
作法一:如图2,作$\angle MDN = \alpha$,过点$D$作$DP \perp DN$,在射线$DP$上截取$DG = a$。过点$G$作$GE \perp DG$,交射线$DM$于点$E$。以点$D$为圆心,$DE$的长为半径画弧,交直线$GE$于点$F$,连接$DF$。则$\triangle DEF$即为所作。
作法二:如图3,作直线$MN$,在直线$MN$上任取一点$O$,过点$O$作直线$MN$的垂线$l$,在直线$l$上截取$OD = a$。作$\angle MOP = \alpha$,作$OD$的垂直平分线,交射线$OP$于点$Q$,连接$DQ$并延长交直线$MN$于点$E$。以点$D$为圆心,$DE$的长为半径画弧,交直线$MN$于点$F$,连接$DF$。则$\triangle DEF$即为所作。
作法三:如图4,作直线$l_1$,在直线$l_1$上任取一点$O$,过点$O$作直线$l_1$的垂线$l_2$,在垂线$l_2$上截取$OD = a$。作$\angle \alpha$的余角$\angle \beta$,作$\angle ODE = \beta$,交直线$l_1$于点$E$。以点$D$为圆心,$DE$长为半径画弧,交直线$l_1$于点$F$,连接$DF$。则$\triangle DEF$即为所作。
图略。
查看更多完整答案,请扫码查看


