例3 (徐州市期末)点$P(1,-2)$关于y轴对称的点的坐标为
分析 根据关于y轴对称的点的特点即可解答.
答案$(-1,-2)$
$(-1,-2)$
.分析 根据关于y轴对称的点的特点即可解答.
答案$(-1,-2)$
答案:
解:关于y轴对称的点的坐标特点是横坐标互为相反数,纵坐标不变。
点P(1,-2)关于y轴对称的点的横坐标为-1,纵坐标为-2,
所以坐标为(-1,-2)。
答案:(-1,-2)
点P(1,-2)关于y轴对称的点的横坐标为-1,纵坐标为-2,
所以坐标为(-1,-2)。
答案:(-1,-2)
例4 (苏州市太仓市期末)已知线段CD是由线段AB平移得到的,点$A(-1,4)的对应点为C(4,7)$,则点$B(-4,-1)$的对应点D的坐标为(
A.$(1,2)$
B.$(2,9)$
C.$(5,3)$
D.$(-9,-4)$
A
)A.$(1,2)$
B.$(2,9)$
C.$(5,3)$
D.$(-9,-4)$
答案:
【解析】:
本题考查了坐标与图形变化中的平移问题。
由于点$A(-1,4)$平移后到达点$C(4,7)$,可以通过比较这两点的坐标来确定平移的规律。
在$x$轴方向上,点$A$的坐标从$-1$变为了$4$,变化了$4-(-1)=5$个单位长度,且是向右平移。
在$y$轴方向上,点$A$的坐标从$4$变为了$7$,变化了$7-4=3$个单位长度,且是向上平移。
所以平移规律是先向右平移$5$个单位长度,再向上平移$3$个单位长度。
接下来,应用这个平移规律来找出点$B(-4,-1)$平移后的坐标。
在$x$轴方向上,点$B$的坐标从$-4$向右平移$5$个单位长度,变为$-4+5=1$。
在$y$轴方向上,点$B$的坐标从$-1$向上平移$3$个单位长度,变为$-1+3=2$。
因此,点$B(-4,-1)$平移后的对应点$D$的坐标为$(1,2)$。
【答案】:
A.$(1,2)$
本题考查了坐标与图形变化中的平移问题。
由于点$A(-1,4)$平移后到达点$C(4,7)$,可以通过比较这两点的坐标来确定平移的规律。
在$x$轴方向上,点$A$的坐标从$-1$变为了$4$,变化了$4-(-1)=5$个单位长度,且是向右平移。
在$y$轴方向上,点$A$的坐标从$4$变为了$7$,变化了$7-4=3$个单位长度,且是向上平移。
所以平移规律是先向右平移$5$个单位长度,再向上平移$3$个单位长度。
接下来,应用这个平移规律来找出点$B(-4,-1)$平移后的坐标。
在$x$轴方向上,点$B$的坐标从$-4$向右平移$5$个单位长度,变为$-4+5=1$。
在$y$轴方向上,点$B$的坐标从$-1$向上平移$3$个单位长度,变为$-1+3=2$。
因此,点$B(-4,-1)$平移后的对应点$D$的坐标为$(1,2)$。
【答案】:
A.$(1,2)$
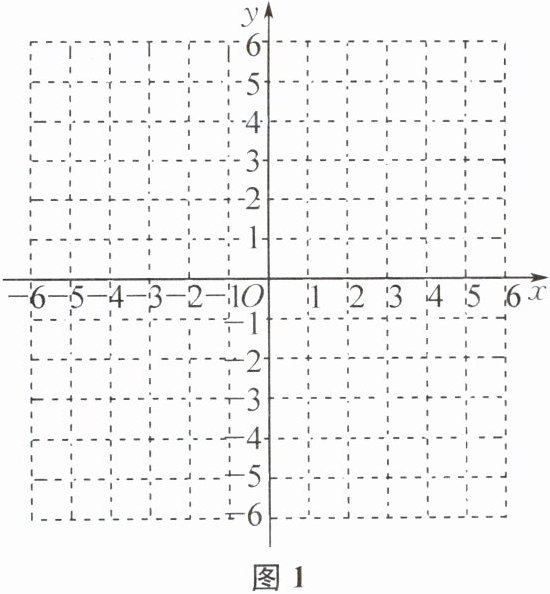
例5 (南京市联合体期末)如图1,在平面直角坐标系中,已知点$A(1,4),B(4,4),C(2,1)$.
(1)请在图中画出$\triangle ABC$;
(2)将$\triangle ABC$向左平移5个单位长度,再沿x轴翻折得到$\triangle A_{1}B_{1}C_{1}$,请在图中画出$\triangle A_{1}B_{1}C_{1}$;
(3)若$\triangle ABC内有一点P(a,b)$,则点P经上述平移、翻折后得到的点$P_{1}$的坐标是____.
(1)请在图中画出$\triangle ABC$;
(2)将$\triangle ABC$向左平移5个单位长度,再沿x轴翻折得到$\triangle A_{1}B_{1}C_{1}$,请在图中画出$\triangle A_{1}B_{1}C_{1}$;
(3)若$\triangle ABC内有一点P(a,b)$,则点P经上述平移、翻折后得到的点$P_{1}$的坐标是____.

答案:
解:
(1)如图2,$\triangle ABC$即为所求.
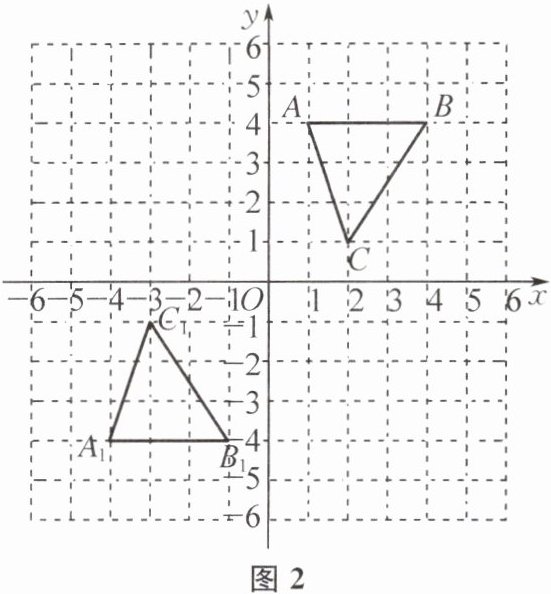
(2)如图2,$\triangle A_{1}B_{1}C_{1}$即为所求.
(3)$(a-5,-b)$
解:
(1)如图2,$\triangle ABC$即为所求.

(2)如图2,$\triangle A_{1}B_{1}C_{1}$即为所求.
(3)$(a-5,-b)$
查看更多完整答案,请扫码查看


