《2025年小题狂做八年级数学上册苏科版提优版》

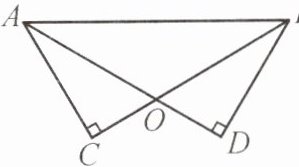
例8 (泰州市泰兴市期末)如图,已知$AD$,$BC相交于点O$,$AD = BC$,$\angle C = \angle D = 90^{\circ}$.求证：
(1)$\triangle ABC\cong\triangle BAD$；
(2)$CO = DO$.

答案：
(1)证明：在$\text{Rt}\triangle ABC$和$\text{Rt}\triangle BAD$中，
$\begin{cases} BC=AD, \\ AB=BA, \end{cases}$
$\therefore \text{Rt}\triangle ABC\cong\text{Rt}\triangle BAD(\text{HL})$。
(2)证明：$\because \text{Rt}\triangle ABC\cong\text{Rt}\triangle BAD$，
$\therefore AC=BD$。
在$\triangle AOC$和$\triangle BOD$中，
$\begin{cases} \angle C=\angle D, \\ \angle AOC=\angle BOD, \\ AC=BD, \end{cases}$
$\therefore \triangle AOC\cong\triangle BOD(\text{AAS})$，
$\therefore CO=DO$。

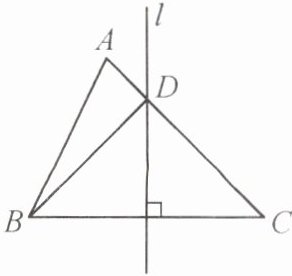
例9 (南京市期末)如图,在$\triangle ABC$中,$AB + AC = 6\ \text{cm}$,$BC的垂直平分线l与AC相交于点D$,则$\triangle ABD$的周长为6$\text{cm}$.

答案： 【解析】：
由题可知，$l$是$BC$的垂直平分线，根据垂直平分线的性质：垂直平分线上任意一点，到线段两端点的间隔相等，所以$DB=DC$，
$\triangle ABD$的周长为$AB+AD+DB$，其中$AD+DB=AD+DC=AC$，
已知$AB+AC=6cm$，所以$\triangle ABD$的周长为$6cm$。
【答案】：
6。