1.(扬州市仪征市期末)在平面直角坐标系中,作点$A(4,3)$关于x轴对称的点$A'$,再将点$A'$向左平移5个单位长度,得到点B,则点B的坐标为(
A.$(-1,-3)$
B.$(1,-3)$
C.$(-3,1)$
D.$(-9,3)$
A
)A.$(-1,-3)$
B.$(1,-3)$
C.$(-3,1)$
D.$(-9,3)$
答案:
A
2.(泰州市兴化市期末)若点P的坐标为$(m+1,m-2)$,则点P不可能在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
B 提示:令m+1=0,则m=-1;令m-2=0,则m=2.分三种情况讨论:当m>2时,m+1>0,m-2>0,则点P在第一象限;当m<-1时,m+1<0,m-2<0,则点P在第三象限;当-1<m<2时,m+1>0,m-2<0,则点P在第四象限.
3.(泰州市高港区期末)在平面直角坐标系中,若点$M(t-3,5-t)$在坐标轴上,则$t= $
3或5
.
答案:
3或5
4.(无锡市期末)如图,在平面直角坐标系中,点A,B的坐标分别为$(3,2),(-1,0)$.若将线段BA绕点B顺时针旋转$90^{\circ }得到线段BA'$,则点$A'$的坐标为____.
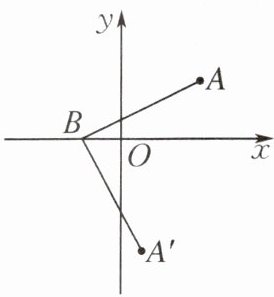

答案:
(1,-4) 提示:如图,过点A作AC⊥x轴于点C.根据题意,得AC=2,BC=4.将Rt△BAC绕点B顺时针旋转90°得到Rt△BA'C',所以BC'=4,A'C'=2,所以点A'的坐标为(1,-4).
(1,-4) 提示:如图,过点A作AC⊥x轴于点C.根据题意,得AC=2,BC=4.将Rt△BAC绕点B顺时针旋转90°得到Rt△BA'C',所以BC'=4,A'C'=2,所以点A'的坐标为(1,-4).

5.(南京市玄武区期末)在平面直角坐标系中,$\triangle ABC$的位置如图所示,直线l经过点$(0,1)$,并与x轴平行,$\triangle A_{1}B_{1}C_{1}与\triangle ABC$关于直线l对称.
(1)画出$\triangle A_{1}B_{1}C_{1}$;
(2)若点$P(m,n)$在边AC上,则点P关于直线l的对称点$P_{1}$的坐标为____;
(3)在直线l上画出点Q,使得$QA+QC$的值最小.
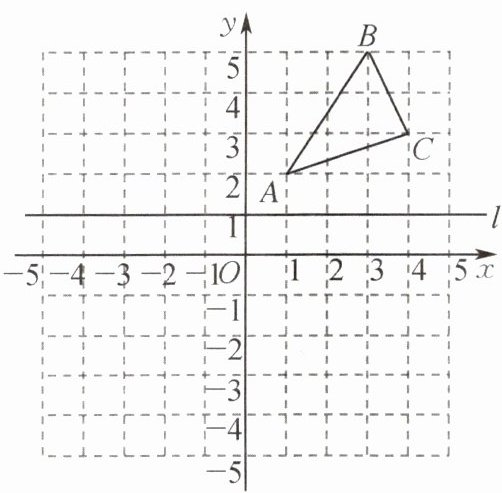
(1)画出$\triangle A_{1}B_{1}C_{1}$;
(2)若点$P(m,n)$在边AC上,则点P关于直线l的对称点$P_{1}$的坐标为____;
(3)在直线l上画出点Q,使得$QA+QC$的值最小.

答案:
解:
(1)如图,△A₁B₁C₁即为所求.
(2)(m,2-n)
(3)如图,点Q即为所求.
解:
(1)如图,△A₁B₁C₁即为所求.
(2)(m,2-n)
(3)如图,点Q即为所求.

6.(苏州市期中节选)如图,在平面直角坐标系中,P是第一象限角平分线上的一点,$OP= \sqrt {2}$,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于B,A两点.
(1)求点P的坐标;
(2)若点A的坐标为$(0,m)$,点B的坐标为$(n,0)$,试判断m,n有什么数量关系,并说明理由.
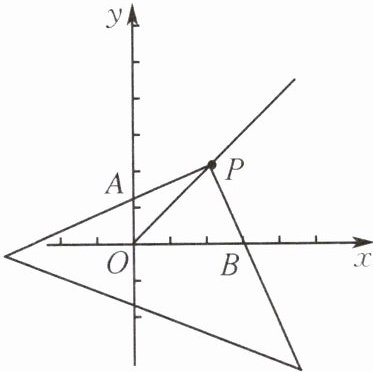
(1)求点P的坐标;
(2)若点A的坐标为$(0,m)$,点B的坐标为$(n,0)$,试判断m,n有什么数量关系,并说明理由.

答案:
解:
(1)过点P作PE⊥x轴于点E.因为P是第一象限角平分线上的一点,所以∠POE=45°,PE=OE.在Rt△PEO中,OP=√2,OP²=OE²+PE²,所以PE=1.所以点P的坐标为(1,1).
(2)m+n=2.理由如下:过点P作PF⊥y轴于点F,则PE⊥PF.易证△APF≌△BPE,所以AF=BE.因为点P的坐标为(1,1),所以OE=OF=1,所以AO+OB=AO+OE+BE=AO+OE+AF=2OE=2.因为点A的坐标为(0,m),点B的坐标为(n,0),所以m+n=2.
(1)过点P作PE⊥x轴于点E.因为P是第一象限角平分线上的一点,所以∠POE=45°,PE=OE.在Rt△PEO中,OP=√2,OP²=OE²+PE²,所以PE=1.所以点P的坐标为(1,1).
(2)m+n=2.理由如下:过点P作PF⊥y轴于点F,则PE⊥PF.易证△APF≌△BPE,所以AF=BE.因为点P的坐标为(1,1),所以OE=OF=1,所以AO+OB=AO+OE+BE=AO+OE+AF=2OE=2.因为点A的坐标为(0,m),点B的坐标为(n,0),所以m+n=2.
查看更多完整答案,请扫码查看


