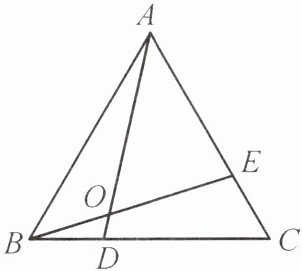
例6 (盐城市东台市期末)如图,$\triangle ABC$是等边三角形,$D$,$E分别是边BC$,$CA$上的点,且$BD = CE$,$AD$,$BE相交于点O$.
(1)求证:$\triangle BAE\cong\triangle ACD$;
(2)求$\angle AOB$的度数.
(1)求证:$\triangle BAE\cong\triangle ACD$;
(2)求$\angle AOB$的度数.

答案:
【解析】:
(1) 要证明$\triangle BAE \cong \triangle ACD$,我们可以按照以下步骤:
第一步,由题目信息,可知$\triangle ABC$是等边三角形,所以$\angle BAC = \angle C = 60^\circ$,且$AB = BC = AC$。
第二步,根据题目条件,$BD = CE$,所以$BC - BD = AC - CE$,即$CD = AE$。
第三步,根据三角形的边角边全等判定,在$\triangle BAE$和$\triangle ACD$中,有$AE = CD$,$\angle BAE = \angle C$,$BA = AC$,所以$\triangle BAE \cong \triangle ACD$。
(2) 要求$\angle AOB$的度数,我们可以按照以下步骤:
第一步,由第一问的结论,可知$\triangle BAE \cong \triangle ACD$,所以$\angle ABE = \angle CAD$。
第二步,根据三角形内角和为$180^\circ$,有$\angle AOB = 180^\circ - \angle BAO - \angle ABO$。
第三步,由于$\angle BAO = \angle BAC - \angle CAD = 60^\circ - \angle CAD$,且$\angle ABO = \angle ABE$,所以$\angle AOB = 180^\circ - (60^\circ - \angle CAD) - \angle ABE = 180^\circ - 60^\circ + \angle CAD - \angle ABE = 120^\circ$(因为$\angle CAD = \angle ABE$)。
或者,我们可以直接利用外角性质,$\angle AOB$是$\triangle AOE$的外角,所以$\angle AOB = \angle OAE + \angle AEO = \angle CAD + \angle ABE + \angle BAC = 60^\circ + 60^\circ = 120^\circ$(因为$\angle CAD = \angle ABE$且$\angle BAC = 60^\circ$)。
【答案】:
(1) 证明:因为$\triangle ABC$是等边三角形,所以$\angle BAC = \angle C = 60^\circ$,$AB = BC = AC$。因为$BD = CE$,所以$CD = AE$。在$\triangle BAE$和$\triangle ACD$中,有
$\begin{cases}AE = CD, \\\angle BAE = \angle C, \\BA = AC,\end{cases}$
所以$\triangle BAE \cong \triangle ACD$(SAS)。
(2) $\angle AOB = 120^\circ$。
(1) 要证明$\triangle BAE \cong \triangle ACD$,我们可以按照以下步骤:
第一步,由题目信息,可知$\triangle ABC$是等边三角形,所以$\angle BAC = \angle C = 60^\circ$,且$AB = BC = AC$。
第二步,根据题目条件,$BD = CE$,所以$BC - BD = AC - CE$,即$CD = AE$。
第三步,根据三角形的边角边全等判定,在$\triangle BAE$和$\triangle ACD$中,有$AE = CD$,$\angle BAE = \angle C$,$BA = AC$,所以$\triangle BAE \cong \triangle ACD$。
(2) 要求$\angle AOB$的度数,我们可以按照以下步骤:
第一步,由第一问的结论,可知$\triangle BAE \cong \triangle ACD$,所以$\angle ABE = \angle CAD$。
第二步,根据三角形内角和为$180^\circ$,有$\angle AOB = 180^\circ - \angle BAO - \angle ABO$。
第三步,由于$\angle BAO = \angle BAC - \angle CAD = 60^\circ - \angle CAD$,且$\angle ABO = \angle ABE$,所以$\angle AOB = 180^\circ - (60^\circ - \angle CAD) - \angle ABE = 180^\circ - 60^\circ + \angle CAD - \angle ABE = 120^\circ$(因为$\angle CAD = \angle ABE$)。
或者,我们可以直接利用外角性质,$\angle AOB$是$\triangle AOE$的外角,所以$\angle AOB = \angle OAE + \angle AEO = \angle CAD + \angle ABE + \angle BAC = 60^\circ + 60^\circ = 120^\circ$(因为$\angle CAD = \angle ABE$且$\angle BAC = 60^\circ$)。
【答案】:
(1) 证明:因为$\triangle ABC$是等边三角形,所以$\angle BAC = \angle C = 60^\circ$,$AB = BC = AC$。因为$BD = CE$,所以$CD = AE$。在$\triangle BAE$和$\triangle ACD$中,有
$\begin{cases}AE = CD, \\\angle BAE = \angle C, \\BA = AC,\end{cases}$
所以$\triangle BAE \cong \triangle ACD$(SAS)。
(2) $\angle AOB = 120^\circ$。
查看更多完整答案,请扫码查看


