3. (泰州市泰兴市期末)如图是一个高为16 m、底面周长为8 m的圆柱形水塔.现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔一周半到达顶端,则登梯至少长
20
m.
答案:
20 提示:设登梯至少长xm.将圆柱表面沿母线切开并展开成长方形,所以x²=(1×8+4)²+16²=400,所以登梯至少长20m.
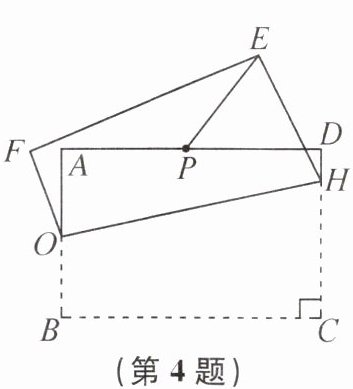
4. (盐城市亭湖区期中)如图,在长方形ABCD中,已知AB= 2,BC= 4,O,P分别是边AB,AD的中点,H是边CD上的一个动点,连接OH.将四边形OBCH沿OH折叠,得到四边形OFEH.连接PE,则PE长的最小值是______.

答案:
√17 - √5 提示:如图,连接EO,PO,OC.由条件,得∠B=∠OAP=90°,OA=OB=1/2 AB=1,AD=BC=4,AP=1/2 AD=2.由轴对称的性质,得OC=OE.因为PE≥OE - OP,所以当点E,P,O共线时,PE的长最小.在Rt△OBC中,由勾股定理,得OC=√(OB²+BC²)=√17,所以OE=√17.在Rt△AOP中,由勾股定理,得OP=√(OA²+AP²)=√5.所以PE长的最小值为OE - OP=√17 - √5.
√17 - √5 提示:如图,连接EO,PO,OC.由条件,得∠B=∠OAP=90°,OA=OB=1/2 AB=1,AD=BC=4,AP=1/2 AD=2.由轴对称的性质,得OC=OE.因为PE≥OE - OP,所以当点E,P,O共线时,PE的长最小.在Rt△OBC中,由勾股定理,得OC=√(OB²+BC²)=√17,所以OE=√17.在Rt△AOP中,由勾股定理,得OP=√(OA²+AP²)=√5.所以PE长的最小值为OE - OP=√17 - √5.

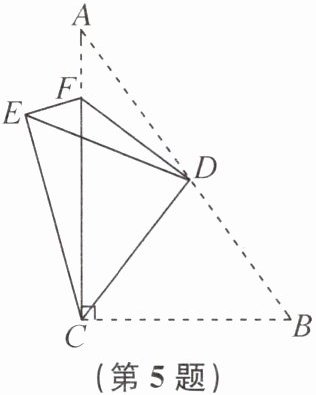
5. (盐城市大丰区期中)如图,在Rt△ABC中,∠ACB= 90°,D为斜边AB的中点,CD= 5,BC= 6,连接CD,将△BCD沿CD所在的直线翻折,使点B落在点E处,F为直角边AC上的一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,则△EFC的面积为______
21/4
.
答案:
21/4 提示:因为∠ACB=90°,D为斜边AB 的中点,CD=5,BC=6,所以AB=10,所以AC=√(AB²−BC²)=8.由翻折可知∠B=∠DEC,∠A=∠DEF,CE=BC=6,AF=EF.因为∠A+∠B=90°,所以∠DEF+∠DEC=90°,即∠FEC=90°.设AF=EF=x,则CF=AC−AF=8−x.在Rt△CEF 中,由勾股定理,得EF²+CE²=CF²,即x²+6²=(8−x)²,解得x=7/4.所以EF=7/4,所以△EFC 的面积为1/2 CE·EF=21/4.
6. (南京市建邺区期末)已知在△ABC中,BC= a,AC= b,AB= c,且c≥b≥a.
(1)当△ABC是锐角三角形时,小明猜想:$a^2+b^2>c^2.$以下是他的证明过程:
小明的证明过程
如图1,过点A作AD⊥CB,垂足为D.
设CD= x.
在Rt△ADC中$,AD^2= b^2-x^2,$
在Rt△ADB中$,AD^2= ① ,$
所以$b^2-x^2= ① ,$
化简,得$a^2+b^2-c^2= 2ax.$
因为a>0,x>0,所以 ② >0,
所以$a^2+b^2-c^2>0,$
所以$a^2+b^2>c^2.$
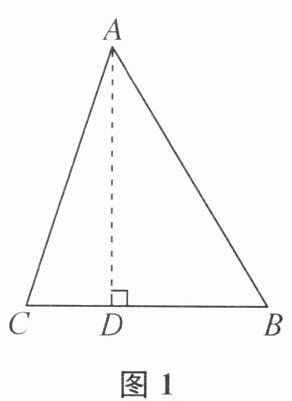
其中,①是______;②是______.
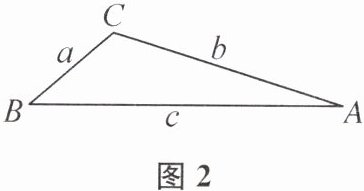
(2)如图2,当△ABC是钝角三角形时,猜想$a^2+b^2$与$c^2$之间的关系并证明.
(1)当△ABC是锐角三角形时,小明猜想:$a^2+b^2>c^2.$以下是他的证明过程:
小明的证明过程
如图1,过点A作AD⊥CB,垂足为D.
设CD= x.
在Rt△ADC中$,AD^2= b^2-x^2,$
在Rt△ADB中$,AD^2= ① ,$
所以$b^2-x^2= ① ,$
化简,得$a^2+b^2-c^2= 2ax.$
因为a>0,x>0,所以 ② >0,
所以$a^2+b^2-c^2>0,$
所以$a^2+b^2>c^2.$

其中,①是______;②是______.
(2)如图2,当△ABC是钝角三角形时,猜想$a^2+b^2$与$c^2$之间的关系并证明.

答案:
(1)c²−(a−x)² 2ax
(2)解:a²+b²<c².证明如下:如图,过点A作AD⊥BC,交BC的延长线于点D.设CD=x.因为在Rt△ADC中,AD²=b²−x²,在Rt△ADB中,AD²=c²−(a+x)²,所以b²−x²=c²−(a+x²,化简,得c²−a²−b²=2ax.因为a>0,x>0,所以2ax>0,所以c²−a²−b²>0,所以c²>a²+b²,即a²+b²<c².
(1)c²−(a−x)² 2ax
(2)解:a²+b²<c².证明如下:如图,过点A作AD⊥BC,交BC的延长线于点D.设CD=x.因为在Rt△ADC中,AD²=b²−x²,在Rt△ADB中,AD²=c²−(a+x)²,所以b²−x²=c²−(a+x²,化简,得c²−a²−b²=2ax.因为a>0,x>0,所以2ax>0,所以c²−a²−b²>0,所以c²>a²+b²,即a²+b²<c².

查看更多完整答案,请扫码查看


