《2025年小题狂做八年级数学上册苏科版提优版》

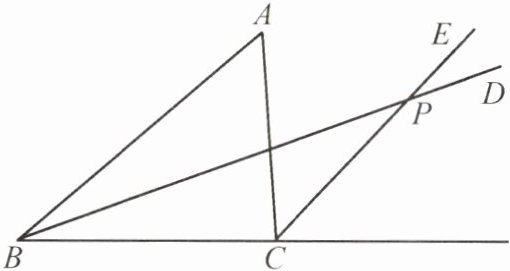
例10 (无锡市期中)如图,在$\triangle ABC$中,$\angle ABC的平分线BD与\angle ACB的邻补角的平分线CE交于点P$.求证：点$P到边AB$,$BC$,$CA$所在直线的距离相等.

答案： 【解析】：
本题主要考查角平分线的性质，即角平分线上的点到角两边的距离相等。
证明过程主要分为以下步骤：
首先，过点$P$作三边$AB$，$BC$，$CA$的垂线，分别交$AB$，$BC$，$CA$于点$Q$，$M$，$N$。
由于点$P$在$\angle ABC$的平分线$BD$上，根据角平分线的性质，有$PQ = PM$。
同样，由于点$P$在$\angle ACM$（$\angle ACB$的邻补角）的平分线$CE$上，再次应用角平分线的性质，有$PM = PN$。
综合以上两步，得出$PQ = PM = PN$，即点$P$到三边$AB$，$BC$，$CA$的距离相等。
【答案】：
证明：过点$P$作边$AB$，$BC$，$CA$所在直线的垂线，垂足分别是$Q$，$M$，$N$。
$\because P$是$\angle ABC$的平分线$BD$上的一点，
根据角平分线的性质，角平分线上的点到角两边的距离相等，
$\therefore PQ = PM$。
$\because P$是$\angle ACM$的平分线$CE$上的一点，
同样根据角平分线的性质，
$\therefore PM = PN$。
$\therefore PQ = PM = PN$，
即点$P$到边$AB$，$BC$，$CA$所在直线的距离相等。

在等腰三角形$ABC$中,$AB = AC$,中线$BD将这个三角形的周长分为15和12$两个部分,则这个等腰三角形的底边长为(C)
A.7
B.11
C.11或7
D.10或7

答案： 【解析】：
题目考查等腰三角形的性质以及三角形三边关系。
首先，设等腰三角形的底边长为$x$，腰长为$y$。
根据等腰三角形的性质，以及中线的性质，我们可以得到两个可能的方程组：
①$\begin{cases}x+\frac{y}{2}=15,\\y+\frac{y}{2}=12.\end{cases}$
或
②$\begin{cases}x+\frac{y}{2}=12,\\y+\frac{y}{2}=15.\end{cases}$
解方程组①：
从第二个方程，我们可以得到：
$\frac{3y}{2}=12$，
$y=8$，
将$y=8$代入第一个方程，得到：
$x+\frac{8}{2}=15$，
$x=11$，
此时，三角形的三边长为$11$，$8$，$8$。
根据三角形的三边关系，任意两边之和大于第三边，所以$8+8＞11$，$8+11＞8$，$11+8＞8$，满足三角形的三边关系。
解方程组②：
从第二个方程，我们可以得到：
$\frac{3y}{2}=15$，
$y=10$，
将$y=10$代入第一个方程，得到：
$x+\frac{10}{2}=12$，
$x=7$，
此时，三角形的三边长为$7$，$10$，$10$。
同样根据三角形的三边关系，$10+10＞7$，$10+7＞10$，$7+10＞10$，也满足三角形的三边关系。
因此，等腰三角形的底边长可以是$11$或$7$。
【答案】：
C