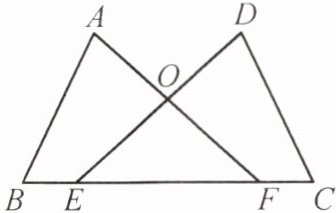
例7 (泰州市姜堰区期中)如图,已知点$E$,$F在线段BC$上,$BE = CF$,$\angle A = \angle D$,$\angle B = \angle C$,$AF与DE交于点O$.求证:$\triangle ABF\cong\triangle DCE$.

答案:
【解析】:题目考查了三角形全等的判定方法,具体为“AAS”(两角及非夹边对应相等)的判定定理。根据题目给出的条件,我们知道两组角对应相等,即$\angle A = \angle D$和$\angle B = \angle C$。同时,通过$BE = CF$,我们可以推导出$BF = CE$,这是通过线段相加得到的。有了这些条件,我们就可以利用“AAS”判定定理来证明两个三角形全等。
【答案】: 证明:
因为$BE = CF$,
所以$BE + EF = CF + EF$,
即$BF = CE$。
在$\triangle ABF$和$\triangle DCE$中,
$\begin{cases}\angle A = \angle D, \\\angle B = \angle C, \\BF = CE.\end{cases}$
所以$\triangle ABF \cong \triangle DCE(AAS)$。
【答案】: 证明:
因为$BE = CF$,
所以$BE + EF = CF + EF$,
即$BF = CE$。
在$\triangle ABF$和$\triangle DCE$中,
$\begin{cases}\angle A = \angle D, \\\angle B = \angle C, \\BF = CE.\end{cases}$
所以$\triangle ABF \cong \triangle DCE(AAS)$。
查看更多完整答案,请扫码查看


